1. 彩色图像处理

1.1. 彩色空间

RGB
- CCD技术直接感知R,G,B三个分量
- 是图像成像、显示、打印等设备的基础
CMY(青、深红、黄)、CMYK (青、深红、黄、黑)
- 运用在大多数在纸上沉积彩色颜料的设备，如彩色打印机和复印机
- CMYK
  - 打印中的主要颜色是黑色
  - 等量的CMY原色产生黑色，但不纯
  - 在CMY基础上，加入黑色，形成CMYK彩色空间
- HSV
  - Hue 、Saturation、Value (色调、饱和度、数值)
  - 基于圆柱坐标系的颜色模型
    - 圆锥体来表示HSV
    - 圆锥的顶面对应于V=1
    - 色彩H由绕V轴的旋转角给定。
    - 红色对应于角度0° ，绿色对应于角度120°，蓝色对应于角度240°
    - 饱和度S取值从0到1，所以圆锥顶面的半径为1
  - HSI(色调、饱和度、亮度）
    - 两个特点：
      - I 分量与图像的彩色信息无关
      - H和S分量与人感受颜色的方式是紧密相连的
    - 将亮度( I )与色调（H）和饱和度（S）分开
    - 避免颜色受到光照明暗(I)等条件的干扰
    - 仅仅分析反映色彩本质的色调和饱和度
    - 广泛用于计算机视觉、图像检索和视频检索
  - YIQ
    - Y指亮度(Brightness),即灰度值
    - I和Q指色调，描述色彩及饱和度
    - 用于彩色电视广播，被北美的电视系统所采用（属于NTSC系统）
    - Y分量可提供黑白电视机的所有影像信息
  - YUV
    - Y指亮度,与YIQ的Y相同
    - U和V也指色调，不同于YIQ的I和Q
    - 用于彩色电视广播，被欧洲的电视系统所采用（属于PAL系统）
    - Y分量也可提供黑白电视机的所有影像信息
  - YCbCr
    - Y指亮度,与YIQ和YUV的Y相同
    - Cb和Cr由U和V调整得到
    - JPEG采用的彩色空间
  - CLE Lab
    - 国际照明委员会制定的色彩模式
    - 自然界中任何一点色可以在Lab空间表达出来
    - 色彩空间比RGB空间大
      - Lab 颜色模型取坐标Lab
      - L：亮度(lightness)
      - a：正数代表红色，负数代表绿色
      - b：正数代表黄色，负数代表蓝色
    - 以数字化的方式来描述人的视觉感应
      - 与设备无关
      - 弥补了RGB和CMYK模式必须依赖设备色彩特性的不足

1.2. 彩色空间转换

RGB -> CMY $\biggr[ \begin{matrix} C \\ M \\ Y \\ \end{matrix}\biggr] = \biggr[ \begin{matrix} 1 \\ 1 \\ 1 \end{matrix} \biggr] - \biggr[ \begin{matrix} R \\ G \\ B \end{matrix} \biggr]$ $[ C M Y ] = [ 1 1 1 ] - [ R G B ]$
- RGB 和 CMY 值都归一化[0,1]
- 在Matlab中，可以通过指令“imcomplement”实现RGB格式的图像与CMY格式图像的转换?
- RGB模型

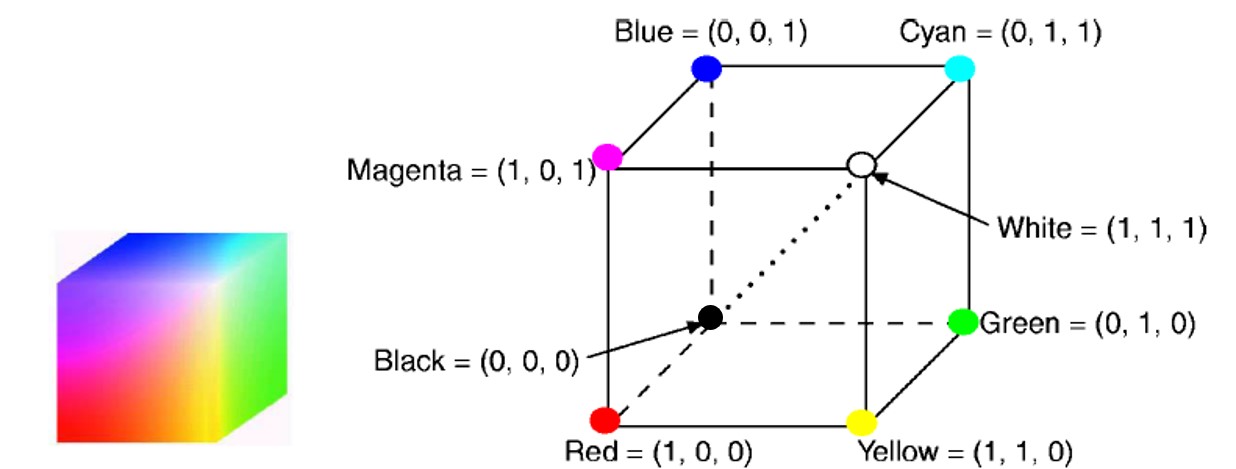
# RGB颜色模型
function rgbcube(vx, vy, vz)
%RGBCUBE Displays an RGB cube on the MATLAB desktop.
%   RGBCUBE(VX, VY, VZ) displays an RGB color cube, viewed from point
%   (VX, VY, VZ).  With no input arguments, RGBCUBE uses (10, 10, 4)
%   as the default viewing coordinates.  To view individual color
%   planes, use the following viewing coordinates, where the first
%   color in the sequence is the closest to the viewing axis, and the 
%   other colors are as seen from that axis, proceeding to the right
%   right (or above), and then moving clockwise. 
%
%      -------------------------------------------------
%           COLOR PLANE                  ( vx,  vy,  vz)
%      -------------------------------------------------
%       Blue-Magenta-White-Cyan          (  0,   0,  10)
%       Red-Yellow-White-Magenta         ( 10,   0,   0)
%       Green-Cyan-White-Yellow          (  0,  10,   0)
%       Black-Red-Magenta-Blue           (  0, -10,   0)
%       Black-Blue-Cyan-Green            (-10,   0,   0)
%       Black-Red-Yellow-Green           (  0,   0, -10)
%
% Set up parameters for function patch.
vertices_matrix = [0 0 0;0 0 1;0 1 0;0 1 1;1 0 0;1 0 1;1 1 0;1 1 1];
faces_matrix = [1 5 6 2;1 3 7 5;1 2 4 3;2 4 8 6;3 7 8 4;5 6 8 7];
colors = vertices_matrix; 
% The order of the cube vertices was selected to be the same as 
% the  order of the (R,G,B) colors (e.g., (0,0,0) corresponds to 
% black, (1,1,1) corresponds to white, and so on.)

% Generate RGB cube using function patch.
patch('Vertices', vertices_matrix, 'Faces', faces_matrix, ...
      'FaceVertexCData', colors, 'FaceColor', 'interp', ...
      'EdgeAlpha', 0) 

% Set up viewing point.
if nargin == 0
   vx = 10; vy = 10; vz = 4;
elseif nargin ~= 3
   error('Wrong number of inputs.')
end
axis off
view([vx, vy, vz])
axis square

HSI模型
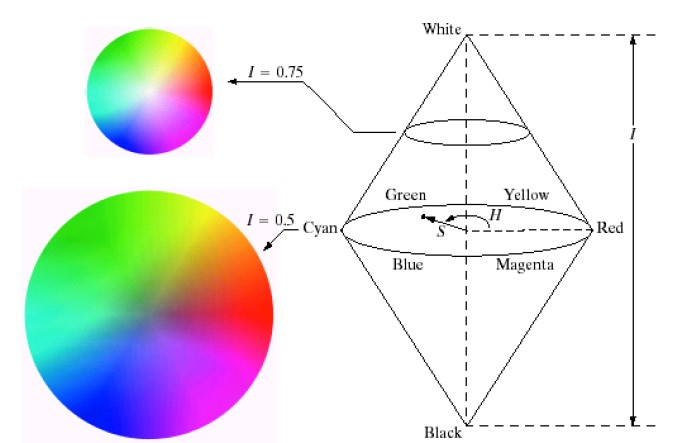
- HSI → RGB $\begin{matrix} 0 \le H \le 2\pi/3 \\ R = I\biggr[1 + \frac{S \cdot \cos(H)}{\cos(\pi/3 -H)}\biggr]\\ G = 3\cdot I -(R+B)\\ B = I\cdot (1-S) \end{matrix}$ $\begin{matrix} 2\pi /3 \le H \le 4\pi/3 \\ G = I\biggr[1 + \frac{S \cdot \cos(H)}{\cos(\pi/3 -H)}\biggr]\\ B = 3\cdot I -(R+G)\\ R = I\cdot (1-S) \end{matrix}$ $\begin{matrix} 4\pi/3 \le H \le 2\pi \\ B = I\biggr[1 + \frac{S \cdot \cos(H)}{\cos(\pi/3 -H)}\biggr]\\ R = 3\cdot I -(R+B)\\ G = I\cdot (1-S) \end{matrix}$
HSI → RGB

# HSI转换为RGB模型
function rgb = hsi2rgb(hsi)
%HSI2RGB Converts an HSI image to RGB.
%   RGB = HSI2RGB(HSI) converts an HSI image to RGB, where HSI is
%   assumed to be of class double with:  
%     hsi(:, :, 1) = hue image, assumed to be in the range
%                    [0, 1] by having been divided by 2*pi.
%     hsi(:, :, 2) = saturation image, in the range [0, 1].
%     hsi(:, :, 3) = intensity image, in the range [0, 1].
%
%   The components of the output image are:
%     rgb(:, :, 1) = red.
%     rgb(:, :, 2) = green.
%     rgb(:, :, 3) = blue.

%   Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
%   Digital Image Processing Using MATLAB, Prentice-Hall, 2004
%   $Revision: 1.5 $  $Date: 2003/10/13 01:01:06 $

% Extract the individual HSI component images.
H = hsi(:, :, 1) * 2 * pi;
S = hsi(:, :, 2);
I = hsi(:, :, 3);

% Implement the conversion equations.
R = zeros(size(hsi, 1), size(hsi, 2));
G = zeros(size(hsi, 1), size(hsi, 2));
B = zeros(size(hsi, 1), size(hsi, 2));

% RG sector (0 <= H < 2*pi/3).
idx = find( (0 <= H) & (H < 2*pi/3));
B(idx) = I(idx) .* (1 - S(idx));
R(idx) = I(idx) .* (1 + S(idx) .* cos(H(idx)) ./ ...
                                          cos(pi/3 - H(idx)));
G(idx) = 3*I(idx) - (R(idx) + B(idx));

% BG sector (2*pi/3 <= H < 4*pi/3).
idx = find( (2*pi/3 <= H) & (H < 4*pi/3) );
R(idx) = I(idx) .* (1 - S(idx));
G(idx) = I(idx) .* (1 + S(idx) .* cos(H(idx) - 2*pi/3) ./ ...
                    cos(pi - H(idx)));
B(idx) = 3*I(idx) - (R(idx) + G(idx));

% BR sector.
idx = find( (4*pi/3 <= H) & (H <= 2*pi));
G(idx) = I(idx) .* (1 - S(idx));
B(idx) = I(idx) .* (1 + S(idx) .* cos(H(idx) - 4*pi/3) ./ ...
                                           cos(5*pi/3 - H(idx)));
R(idx) = 3*I(idx) - (G(idx) + B(idx));

% Combine all three results into an RGB image.  Clip to [0, 1] to
% compensate for floating-point arithmetic rounding effects.
rgb = cat(3, R, G, B);
rgb = max(min(rgb, 1), 0);

RGB → HSI

$\theta = \arccos\frac{\frac{1}{2}\cdot [(R-G)+(R-B)]}{\sqrt{(R-G)^2 + (R-G)\cdot(R-B)}}$

$H = \biggr\{\begin{matrix} \theta & B \le G \\ 360- \theta & B \gt G \\ \end{matrix}$

$S = 1- \frac{3}{R+G+B}\min{(R,G,B)}$

$I = \frac{1}{3}(R+G+B)$

  # RGB转换为HSI模型
  function hsi = rgb2hsi(rgb)
  %RGB2HSI Converts an RGB image to HSI.
  %   HSI = RGB2HSI(RGB) converts an RGB image to HSI. The input image
  %   is assumed to be of size M-by-N-by-3, where the third dimension
  %   accounts for three image planes: red, green, and blue, in that
  %   order. If all RGB component images are equal, the HSI conversion
  %   is undefined. The input image can be of class double (with values
  %   in the range [0, 1]), uint8, or uint16. 
  %
  %   The output image, HSI, is of class double, where:
  %     hsi(:, :, 1) = hue image normalized to the range [0, 1] by
  %                    dividing all angle values by 2*pi. 
  %     hsi(:, :, 2) = saturation image, in the range [0, 1].
  %     hsi(:, :, 3) = intensity image, in the range [0, 1].

  %   Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
  %   Digital Image Processing Using MATLAB, Prentice-Hall, 2004
  %   $Revision: 1.5 $  $Date: 2005/01/18 13:44:59 $

  % Extract the individual component images.
  rgb = im2double(rgb);
  r = rgb(:, :, 1);
  g = rgb(:, :, 2);
  b = rgb(:, :, 3);

  % Implement the conversion equations.
  num = 0.5*((r - g) + (r - b));
  den = sqrt((r - g).^2 + (r - b).*(g - b));
  theta = acos(num./(den + eps));

  H = theta;
  H(b > g) = 2*pi - H(b > g);
  H = H/(2*pi);

  num = min(min(r, g), b);
  den = r + g + b;
  den(den == 0) = eps;
  S = 1 - 3.* num./den;

  H(S == 0) = 0;

  I = (r + g + b)/3;

  % Combine all three results into an hsi image.
  hsi = cat(3, H, S, I);

RGB → YIQ $\biggr[ \begin{matrix} Y \\ I \\ Q \end{matrix} \biggr] = \biggr[ \begin{matrix} 0.299 & 0.587 & 0.114 \\ 0.596 & -0.274 & -0.322 \\ 0.211 & -0.523 & 0.312 \end{matrix} \biggr] \cdot \biggr[\begin{matrix} R \\ G\\B \end{matrix}\biggr]$ $[ Y I Q ] = [ 0.299 0.596 0.211 0.587 - 0.274 - 0.523 0.114 - 0.322 0.312 ] \cdot [ R G B ]$
- 从RGB格式图像到YIQ格式图像实现通过指令“rgb2ntsc”
YIQ → RGB $\biggr[ \begin{matrix} R \\ G \\ B \end{matrix} \biggr] = \biggr[ \begin{matrix} 1 & 0.956 & 0.621 \\ 1 & -0.272 & -0.647 \\ 1 & -1.106 & 1.703 \end{matrix} \biggr] \cdot \biggr[\begin{matrix} Y \\ I\\ Q \end{matrix}\biggr]$
- 从YIQ格式图像到RGB格式图像实现通过指令“ntsc2rgb”
RGB → YUV $\biggr[ \begin{matrix} Y \\ U \\ V \end{matrix} \biggr] = \biggr[ \begin{matrix} 0.299 & 0.587 & 0.114 \\ -0.148 & -0.289 & 0.437 \\ 0.615 & -0.515 & -0.1 \end{matrix} \biggr] \cdot \biggr[\begin{matrix} R \\ G\\ B \end{matrix}\biggr]$
YUV → RGB $\biggr[ \begin{matrix} R \\ G \\ B \end{matrix} \biggr] = \biggr[ \begin{matrix} 1 & 0 & 1.140 \\ 1 & -0.395 & -0.581 \\ 1 & 2.032 & 0 \end{matrix} \biggr] \cdot \biggr[\begin{matrix} Y \\ U\\ V \end{matrix}\biggr]$
RGB → YCbCr $\biggr[ \begin{matrix} Y \\ Cb \\ Cr \\ 1 \end{matrix} \biggr] = \biggr[ \begin{matrix} 0.2990 & 0.5870 & 1.1140 & 0 \\ -0.1687 & -0.3313 & 0.5 & 128\\ 0.5 & -0.4187 & -0.0813 & 128 \\ 0 & 0 & 0 & 1 \end{matrix} \biggr] \cdot \biggr[\begin{matrix} R \\ G\\ B \\ 1 \end{matrix}\biggr]$
- 从 RGB 到 YCbCr 通过指令 “rgb2ycbcr” 来实现
YCbCr → RGB $\biggr[ \begin{matrix} R \\ G \\ B \end{matrix} \biggr] = \biggr[ \begin{matrix} 1 & 1.402 & 0 \\ 1 & -0.34414 & -0.71414 \\ 1 & 1.772 & 0 \end{matrix} \biggr] \cdot \biggr[\begin{matrix} Y \\ Cb-128\\ Cr-128 \end{matrix}\biggr]$
- 从 YCbCr 到 RGB 通过指令 “ycbcr2rgb” 来实现
RGB → CIE Lab
- CIE Lab 模型 (1976 CIE 提出)
  - Lab系统是在三维坐标系统上的,基于一种对称理论，即使用black-white L, red-green a,yellow-blue b 模块
  - 它与具体设备无关的 $L^{*}=116f(\frac{Y}{Y_{n}})-16$ $a^{*} = 500 \cdot \biggr[f(\frac{X}{X_{n}})-f(\frac{Y}{Y_{n}})\biggr]$ $b^{*} = 200 \cdot\biggr[f(\frac{Y}{Y_{n}}) - f(\frac{Z}{Z_{n}})\biggr]$ where,
$f(t) = \biggr\{\begin{matrix} \sqrt[3]{t} & if \quad t >(\frac{6}{29})^{3} \\ \frac{t}{3}\times (\frac{29}{6})^{2} + \frac{4}{29} & otherwise \end{matrix}$
- $X_{n}$ , $Y_{n}$ , $Z_{n}$ 是CIE X,Y,Z相对于白色的参考三色值
- RGB 模型与CLE Lab* 模型，能够通过指令"makecform"和"applycform"来实现
```
clc;
clear;
imRGB = imread('../pic/7.jpg');
figure;
imshow(imRGB);title('原始RGB图像');
cform = makecform('srgb2lab','AdaptedWhitePoint', whitepoint('D65'));
imLab = applycform(imRGB, cform);
figure;
imshow(imLab);title('Lab模型图像');
cform2 = makecform('lab2srgb','AdaptedWhitePoint', whitepoint('D65'));
rgb = applycform(imLab,cform2);
figure;
imshow(rgb);title('Lab模型到RGB图像');
```

1.3. 伪彩色处理

什么叫伪彩色图像处理?
- 也叫假彩色图像处理
- 根据一定的准则对灰度值赋以彩色的处理
- 区分：伪彩色图像、真彩色图像、单色图像
为什么需要伪彩色图像处理?
- 人类可以辨别上千种颜色和强度
- 只能辨别二十几种灰度
应用
- 为人们观察和解释图像中的灰度目标
怎样进行伪彩色图像处理？
- 强度分层技术
- 灰度级到彩色转换技术
   1.3.1. 强度分层技术
把一幅图像描述为三维函数（x,y,f(x,y)）
分层技术：放置平行于(x,y)坐标面的平面
每一个平面在相交区域切割图像函数
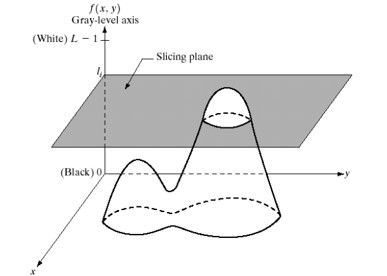
- 令[0,L-1]表示灰度级，使l0代表黑色(f(x , y)=0), $l_{L-1}$代表白色(f(x , y)=L-1)。假设垂直于强度轴的P个平面定义为量级 $l_{1}$ , $l_{2}$ , $l_{3}$ ,…, $l_{p+1}$ ,P个平面将灰度级分为 $P+1$ 个间隔， $V_{1}$ , $V_{2}$ ,..., $V_{P+1}$ ,则灰度级到彩色的赋值关系：
- $c_{k}$ 是与强度间隔 $V_{k}$ 第 $K$ 级强度有关的颜色
- $V_{k}$ 是由在 $l=k-1$ 和 $l=k$ 分割平面定义的
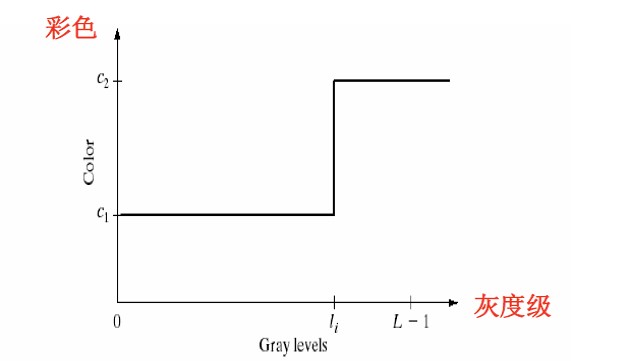
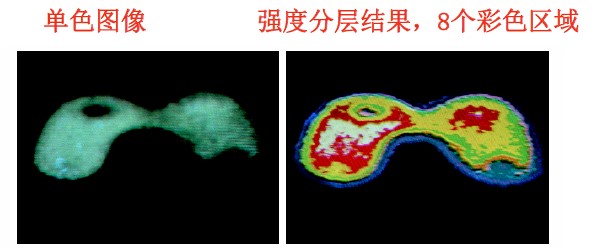
- 左图难以区分病变，右图强度分层结果，清楚的显示恒定强度的不同区域。
- 下图图像的强度值直接与降雨相对应，目测困难
  - 上图：蓝色表示低降雨量，红色表示高降雨量
  - 上面2个图片显得更加清楚

1.3.2. 灰度级到彩色的转换

对任何输入像素的灰度级执行3个独立变换
3个变换结果分别送入彩色监视器的红、绿、蓝三个通道
产生一幅合成图像,matlab实现：Cat(3,R,G,B)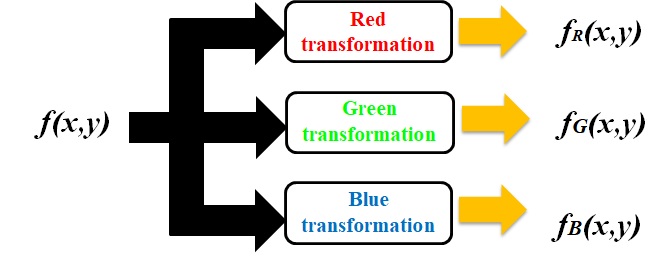

1.4. 全彩色图像处理

全彩色图像处理基础
- 全彩色图像处理研究分为两大类：
  - 分别处理每一分量图像，然后合成彩色图像
  - 直接对彩色像素处理：3个颜色分量表示像素向量。令C代表RGB彩色空间中的任意向量 $C = \biggr[\begin{matrix} C_{R}\\C_{G}\\C_{B} \end{matrix}\biggr] = \biggr[\begin{matrix}R\\G\\B \end{matrix}\biggr]$
- 对大小M×N的图像 $C(x,y) = \biggr[\begin{matrix} C_{R}(x,y)\\C_{G}(x,y)\\C_{B}(x,y) \end{matrix}\biggr] = \biggr[\begin{matrix}R(x,y)\\G(x,y)\\B(x,y) \end{matrix}\biggr]$ $C (x, y) = [ C^{ R } (x, y) C^{ G } (x, y) C^{ B } (x, y) ] = [ R (x, y) G (x, y) B (x, y) ]$
  - 其中：x=0,1,2,…,M-1, y=0,1,2,…,N-1.
彩色变换函数 $g(x,y) = T[f(x,y)]$ $g (x, y) = T [f (x, y)]$
- $f(x,y)$ 是彩色输入图像，$g(x,y)$是变换或者处理过的彩色输出图像, $T$ 是在空间领域 $(x,y)$ 上对 $f$ 的操作
- 彩色变换的简单形式
  - $S_{i}= T_{i}(r_{1}, r_{2},..., r_{n})$ ,其中i= 1,2,...,n。 $r_{i}$ 和 $S_{i}$ 是 $f(x, y)$ 和 $g(x, y)$ 在任何点处彩色分量的变量
  - $\{ T_{1},T_{2},...,T_{n}\}$ 是一个对 $r_{i}$ 操作产生的变换或彩色映射 $S_{i}$ 函数集
  - 选择的彩色空间决定n的值，如RGB彩色空间,n=3, $r_{1}$ , $r_{2}$ , $r_{3}$ 表示红、绿、蓝分量;CMYK,则n=4。

1.5. 彩色图像平滑和锐化

彩色图像平滑
- 令 $S_{xy}$ 表示在RGB彩色图像中定义一个中心在(x,y)的邻域的坐标集，在该邻域中RGB分量的平均值为表示在RGB彩色图像中定义一个中心在 $\overline{c}(x,y) = \frac{1}{k}\sum_{(x,y)\in S_{xy}}c(x,y)$
$\overline{c}(x,y) = \biggr[ \begin{matrix} \frac{1}{K}\sum_{(x,y)\in S_{xy}}R(x,y)\\ \frac{1}{K}\sum_{(x,y)\in S_{xy}}G(x,y)\\ \frac{1}{K}\sum_{(x,y)\in S_{xy}}B(x,y) \end{matrix} \biggr]$

# RGB -> HSI
fc  = imread('../pic/lema.png');
figure;
subplot(221);
imshow(fc)
title('原始真彩色（256*256*256色）图像')
fr = fc(:,:,1);
fg = fc(:,:,2);
fb = fc(:,:,3);
subplot(222);
imshow(fr);
title('红色分量图像');
subplot(223);
imshow(fg);
title('绿色分量图像');
subplot(224);
imshow(fb);
title('蓝色分量图像');
h = rgb2hsi(fc);
H = h(:,:,1);
S = h(:,:,2);
I = h(:,:,3);
figure;
subplot(221);
imshow(h);title('HSI图像');
subplot(222);
imshow(H)
title('色调分量图像');
subplot(223);
imshow(S);
title('饱和度分量图像')
subplot(224);
imshow(I);
title('亮度分量图像');
# 彩色图像平滑
w = fspecial('average',15);
I_filtered = imfilter(I,w,'replicate');
h = cat(3,H,S,I_filtered);
f = hsi2rgb(h);
% f = min(f,1);
figure;
imshow(f);
title('仅平滑HSI图像的亮度分量所得到的RGB图像')
fc_filtered = imfilter(fc,w,'replicate');
figure;
imshow(fc_filtered)
title('分别平滑R、G、B图像分量平面得到的RGB图像');
h_filtered = imfilter(h,w,'replicate');
f = hsi2rgb(h_filtered);
f = min(f,1);figure;
imshow(f)
title('分别平滑H、S、I图像分量平面得到的RGB图像')
h_filtered = imfilter(h,w,'replicate');
figure;
imshow(h_filtered);
title('分别平滑H、S、I图像分量平面得到的HSI图像');

1.5.1. 彩色图像锐化

RGB彩色空间，分别计算每一分量图像的拉普拉斯变换

\nabla [c(x,y)] = \biggr[\begin{matrix} \nabla^{2}R(x,y)\\\nabla^{2}G(x,y)\\\nabla^{2}B(x,y) \end{matrix}\biggr]

g(x,y)=f(x,y)- \nabla^{2}f(x,y) = 5\cdot f(x,y)- \biggr[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)\biggr]

fc  = imread('../pic/2.jpg');
figure;
subplot(231);
imshow(fc);
title('原始真彩色（256*256*256色）图像');
w = fspecial('average',15);
fc_filtered = imfilter(fc,w,'replicate');
subplot(232);
imshow(fc_filtered)
title('分别平滑R、G、B图像分量平面得到的RGB模糊图像')
lapmask = [1 1 1; 1 -8 1; 1 1 1];
fen = imsubtract(fc_filtered,imfilter(fc_filtered,lapmask,'replicate'));
subplot(233);
imshow(fen);
title('用拉普拉斯算子增强模糊图像')
LPA = imfilter(fc,lapmask,'replicate');
subplot(234);
imshow(LPA);
title('对原始真彩色图像用拉普拉斯算子提取出的图像')
fen = imsubtract(fc,imfilter(fc,lapmask,'replicate'));
subplot(235);
imshow(fen);
title('用拉普拉斯算子增强原始真彩色图像（采用提高边缘亮度手段）');

彩色图像处理