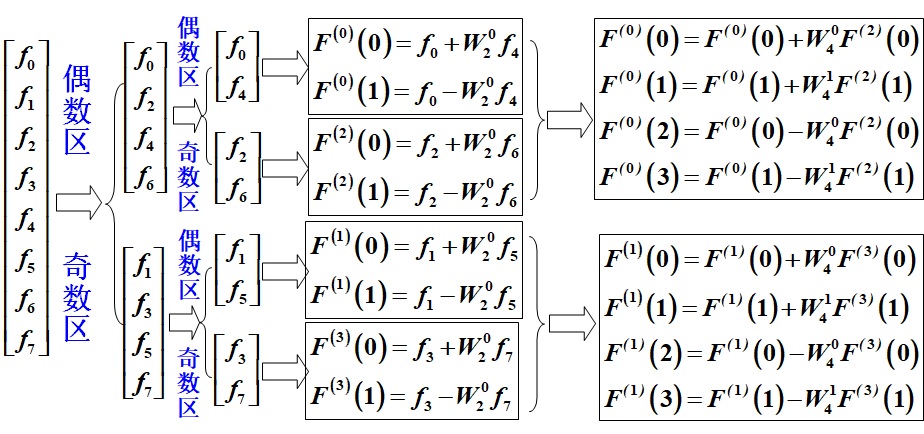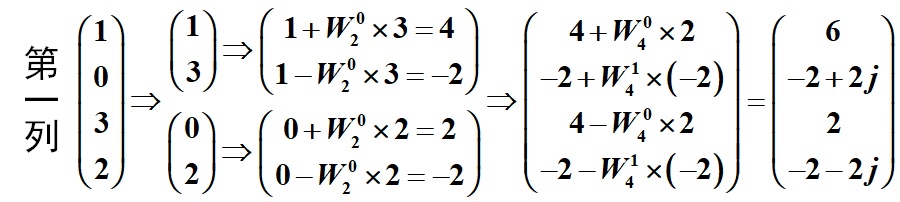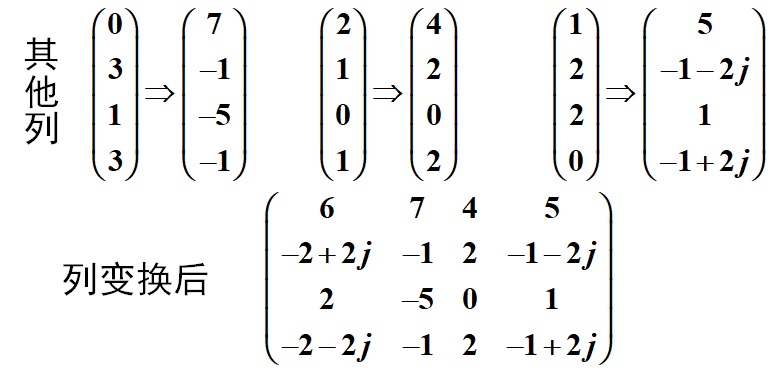1.1. 离散傅里叶变换
f(t)=2a0+∑n=1∞(ancosnωt+bnsinnωt)
ω=T2π
an=T2∫−2T2Tf(t)cosnωtdt
bn=T2∫−2T2Tf(t)sinnωtdt
ejθ=cosθ+jsinθ
容易得到:
cosnωt=2ejnωt+e−jnωt
sinnωt=−j2ejnωt−e−jnωt
带入傅里叶级数中:
f(t)=2a0+∑n=1∞(ancosnωt+bnsinnωt)
f(t)=2a0+∑n=1∞[an×2ejnωt+e−jnωt−bn×j2ejnωt−e−jnωt]
f(t)=2a0+∑n=1∞[2an−jbnejnωt+2an+jbne−jnωt]
令:
c0=2a0cn=2an−jbndn=2an+jbn
则:
f(t)=c0+∑n=1∞(cnejnωt+dne−jnωt)
已知:
c0=T1∫−2T2Tf(t)dt
cn=T1∫−2T2Tf(t)(cosnωt−jsinnωt)dt=T1∫−2T2Tf(t)e−jnωtdt
dn=T1∫−2T2Tf(t)(cosnωt+jsinnωt)dt=T1∫−2T2Tf(t)ejnωtdt
显然:
dn=c−n
则:
∑n=1∞dnejnωt=∑n=1∞c−ne−jnωt=∑n=−∞−1cnejnωt
f(t)=c0+∑n=1∞(cn×ejnωt+dn×e−jnωt)=c0ej0ωt+∑n=1∞(cn×ejnωt+c−n×e−jnωt)
f(t)=c0ej0ωt+∑n=1∞(cn×ejnωt+c−n×e−jnωt)=c0ej0ωt+∑n=1∞(cn×ejnωt)+∑n=−∞−1cn×ejnωt)
f(t)=∑n=−∞+∞cnejnωt
1.1.1. 快速傅里叶变换FFT
一维傅里叶变换DFT
DFT表示为:
F(u)=∑x=0N−1f(x)eN−j2πux,u=0,...,N−1
IDFT表示为:
f(x)=N1∑u=0N−1F(u)eNj2πux,x=0,...,N−1
令
W=eN−j2π
则:
F(u)=∑x=0N−1f(x)Wux,u=0,...,N−1
f(x)=N1∑u=0N−1F(u)W−ux,x=0,...,N−1
因为W因子具有周期性和对称性
Wu±rN=e−j2πNu±rN=e−jN2πu×e∓j2πr=e−jN2πu=Wu
Wu±2N=e−jN2π(u±2N)=e−jN2πu×e∓jπ=−e−jN2πu=−Wu
所以,合理安排重复出现的相乘运算,减少计算工作量
F(u)=∑x=03f(x)Wux=f(0)W0+f(1)W1+f(2)W2+f(3)W3
⎣⎢⎢⎡F(0)F(1)F(2)F(3)⎦⎥⎥⎤=⎣⎢⎢⎡W0W0W0W0W0W1W2W3W0W2W4W6W0W3W6W9⎦⎥⎥⎤=⎣⎢⎢⎡f(0)f(1)f(2)f(3)⎦⎥⎥⎤
W的对称性
W2=−W0
W3=−W1
W的周期性
W4=−W0
W6=−W2
W9=−W1
⎣⎢⎢⎡F(0)F(1)F(2)F(3)⎦⎥⎥⎤=⎣⎢⎢⎡W0W0W0W0W0W1W2W3W0W2W4W6W0W3W6W9⎦⎥⎥⎤⎣⎢⎢⎡f(0)f(1)f(2)f(3)⎦⎥⎥⎤
=⎣⎢⎢⎢⎢⎡11111W1−1−W11−11−11−W1−1W1⎦⎥⎥⎥⎥⎤⎣⎢⎢⎡f(0)f(1)f(2)f(3)⎦⎥⎥⎤
=⎣⎢⎢⎡f(0)+f(2)+(f(1)+f(3))f(0)−f(2)+[f(1)−f(3)]W1f(0)+f(2)−[f(1)+f(3)]f(0)−f(2)−[f(1)−f(3)]W1⎦⎥⎥⎤
F(u)=∑x=0N−1f(x)eN−j2πux=∑x=0N−1f(x)WNux=∑x=0N/2−1f(2x)WN2ux+∑x=0N/2−1f(2x+1)WNu(2x+1)
令
M=2N
则:
F(u)=∑x=0M−1f(2x)WMux+∑x=0M−1f(2x+1)WMuxWNu
F(u)=Fe(u)+WNuFo(u)0≤u≤M
**分成奇数项和偶数项之和**
1.1.2. 总结
将原函数分为奇数项和偶数项,通过不断的一个奇数一个偶数的相加(减),最终得到需要的结果
FFT是将复杂的运算变成两个数相加(减)的简单运算的重复。
F(u)=Fe(u)+WNu+MF0(u)
F(u+M)=Fe(u)−WNuF0(u)
例子:
一个长为8的数字序列,利用FFT算法求其DFT。
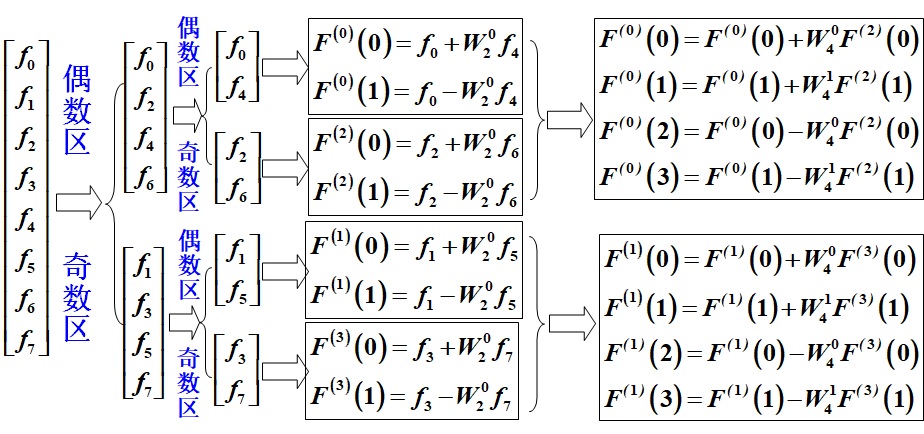
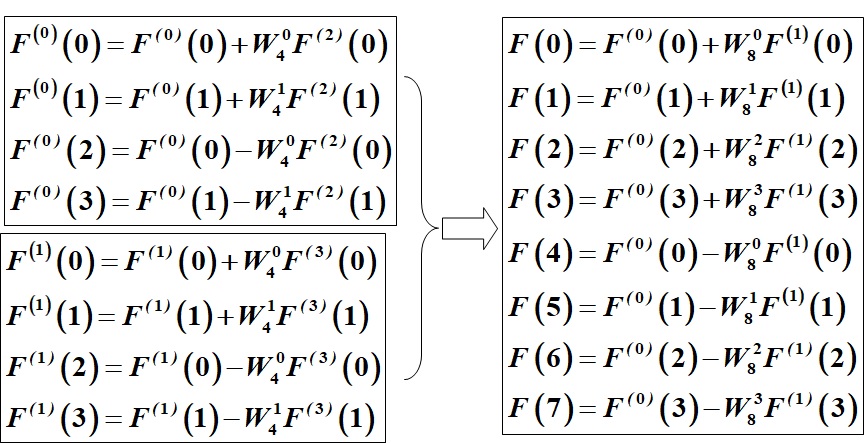
1.1.3. 二维离散傅里叶变换
F(u,v)=∑x=0M−1∑y=0N−1f(x,y)e−j2π(Mxu+Nyv)x,u=0,1,....,M−1y,v=0,1,2...N−1
f(u,v)=MN1∑x=0M−1∑y=0N−1F(u,v)ej2π(Mxu+Nyv)x,u=0,1,....,M−1y,v=0,1,2...N−1
例:

先按列变换(也可以先按行变换)
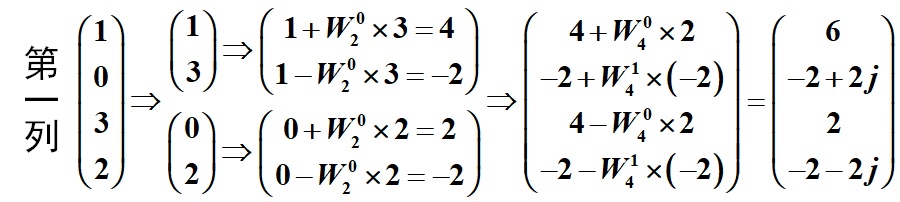
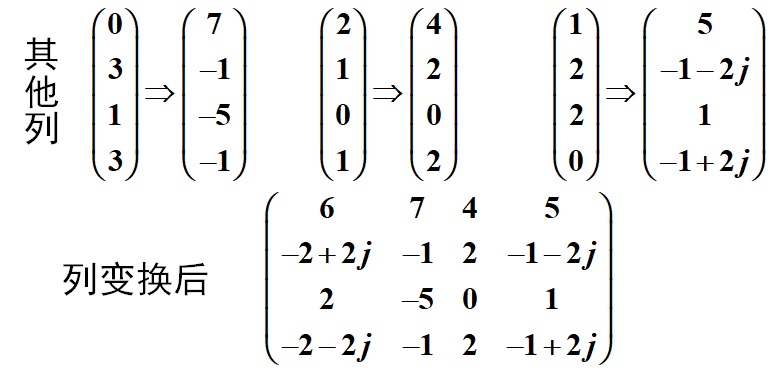

1.1.4. 卷积定理
如果
F(f(t))=F(μ)F(h(t))=H(μ)⇒F[f(t)⋆h(t)]=F(μ)⋅H(μ)