1.1. 直方图处理

1.1.1. 灰度直方图

描述了一副图像的灰度级统计信息，主要应用于图像分割和图像灰度变换等处理过程中。

• 从数学角度来说，图像直方图描述图像各个灰度级的统计特性，它是图像灰度值的函数，统计一幅图像中各个灰度级出现的次数或概率。归一化直方图可以直接反映不同灰度级出现的比率。
• 横坐标为图像中各个像素点的灰度级别，纵坐标表示具有各个灰度级别的像素在图像中出现的次数或概率。

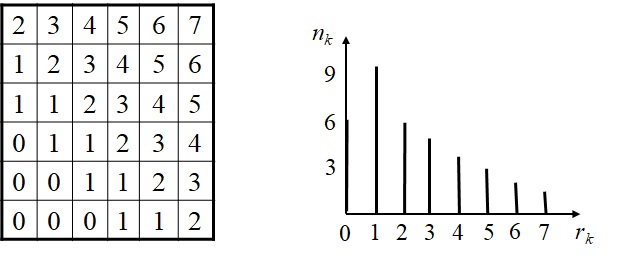
灰度直方图表示的是数字图像中每一灰度级与其出现频数（即该灰度上出现像素的数目）间的统计关系。

即：横坐标表示灰度级，纵坐标表示频数或者相对频数（即该灰度级上像素出现的概率） $p(r_{k})=\frac{n_{k}}{N}$

1.1.2. 灰度直方图性质

• 直方图不具有空间特性。直方图不能反映图像像素空间位置信息。
• 直方图反映图像大致描述。
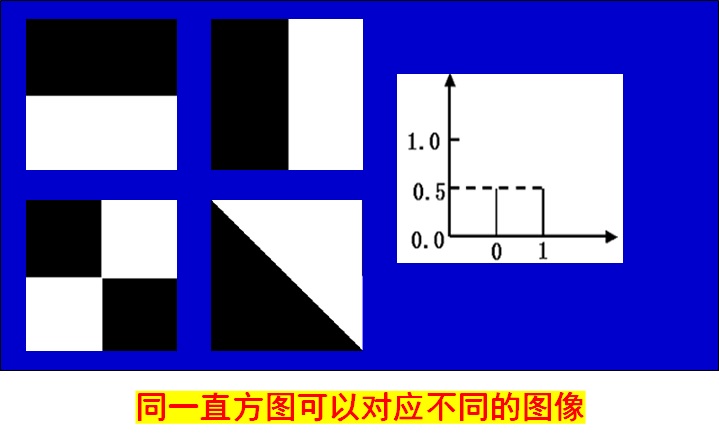
• 一幅图像唯一对应相应的直方图，而不同的图像可以具有相同的直方图。
• 若一幅图像可分为多个子区，则多个子区直方图之和等于对应的全图直方图。

若一幅图像的像素倾向于占据整个可能的灰度级且分布均匀，则该图像会有高对比度的外观并展示灰色调的较大变化，最终效果将是一幅灰度细节丰富且动态范围较大的图像。

• 图像的灰度动态范围太小或者说其直方图集中在某一个灰度区间，视觉效果不理想。
• 当图像直方图占满所有灰度级区间，且所有灰度级的概率分布相接近，即，直方图均匀分布的图像其视觉效果会最理想。
• 另一方面，从随机信号及信息量的角度来看，各个灰度级的概率分布等概率时，信息量最大，熵最大。
• 因此，需要寻找这一个变换，使得变换后图像直方图均匀，这就是直方图均衡化。

1.1.3. 直方图均衡化

设r为要增强像素灰度级，s为增强后新灰度级 $0 \le s \le 1 \quad 0 \le s \le 1$ 直方图修正公式： $s = T(r) \quad r = T^{-1}(s)$ 式中T(r)为变换函数，要满足两个条件：

• T(r)在[0,1]区域内单增，以保证灰度级从黑到白的次序不要出现反转。
• T(r)在[0,1]区域内满足s 在[0,1]范围内，保证变换的像素灰度级仍在允许的灰度级范围内。

关键核心为寻找满足两个条件的变换函数 T(r)

直方图均衡化，又叫做直方图均匀化。其目的是使所有灰度级出现的相对频数(概率)相同，此时图像所包含的信息量最大。 也就是使得原图像的灰度直方图修正为均匀分布的直方图，实现图像的全局整体均匀化。

pr(r)和ps(s)分别表示r和s的灰度概率密度函数

一幅离散数字图像,共L个灰度等级,其中第k个灰度级rk出现的像素个数为nk，图像总像素个数为N。则第k个灰度级出现的概率为： $P(r_{k}) = \frac{n_{k}}{N} \quad 0 \le r_{k} \le 1, k=0,...,L-1$ 进行均衡化处理的变换函数T(r)为： $s_{k} = T(r_{k}) = \sum_{j=0}^{k}p_{r}(r_{j}) = \sum_{j=0}^{k}\frac{n_{j}}{N}$ 且 $r_{k} = T^{-1}(s_{k})$

• 算法步骤

  • 统计原始图像直方图

  • 计算新的灰度级 $s_{k}=T(r_{k})=\sum_{j=0}^{k}p_{r}(r_{j}) = \sum_{j=0}^{k}\frac{n_{j}}{N}$

• 修正sk为合理灰度级

• 求新直方图

• 用处理后的新灰度代替处理前的灰度，生成新图像

​

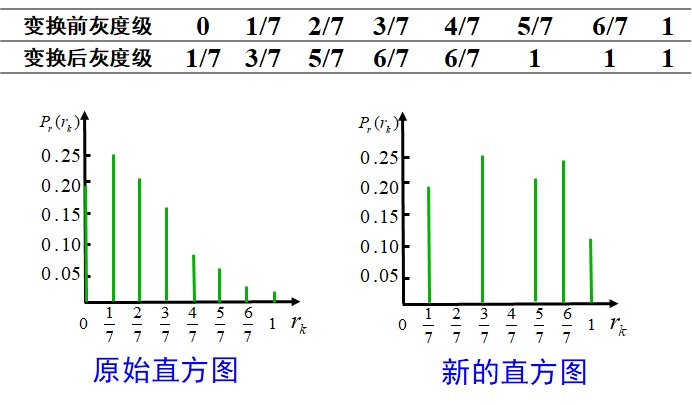
例：

给定一幅64*64的8级灰度图像，其灰度级分布如表所示，对其进行直方图均衡化。

解：由原图灰度分布统计可看出，该图像绝大部分像素灰度值集中在低灰度区，图像整体偏暗。

• 计算新的灰度级

$s_{0} = T(r_{0}) = \sum_{j=0}^{0}p_{r}(r_{j})=P_{r}(r_{0})=0.19$

$s_{1} = T(r_{1}) = \sum_{j=1}^{0}p_{r}(r_{j})=P_{r}(r_{0})+P_{r}(r_{1})=0.19+0.25=0.44$

以此类推： $s_{2} = 0.19+0.25+0.21=0.65$

$s_{3} = 0.19+0.25+0.21+0.16 = 0.81$

$s_{4} =0.19+0.25+0.21+0.16+0.08=0.89$

$s_{5} =0.19+0.25+0.21+0.16+0.08+0.06=0.95 \approx 1$

$s_{6} =0.19+0.25+0.21+0.16+0.08+0.06+0.03=0.98 \approx 1$

$s_{6} =0.19+0.25+0.21+0.16+0.08+0.06+0.03+0.02= 1$

• 修正为合理的灰度级 $s_{0} =0.19 \approx \frac{1}{7}$

  $s_{1} = 0.44 \approx \frac{3}{7}$

  $s_{2} = 0.65 \approx \frac{5}{7}$

  $s_{3} = 0.81 \approx \frac{6}{7}$

  $s_{4} = 0.89 \approx \frac{6}{7}$

  $s_{5} = 0.95\approx 1$

  $s_{6} = 0.98\approx 1$

  $s_{7} = 1$

  则新图像对应只有5个不同的灰度级别 $s_{0}^{'} = \frac{1}{7} \quad s_{1}^{'} = \frac{3}{7} \quad s_{2}^{'} = \frac{5}{7} \quad s_{3}^{'} = \frac{6}{7} \quad s_{4}^{'} = 1$

• 计算新的直方图 $p_{s}(s_{0}^{'})=p_{s}(\frac{1}{7})=p_{r}(r_{0})=0.19$

  $p_{s}(s_{1}^{'})=p_{s}(\frac{3}{7})=p_{r}(r_{1})=0.25$

  $p_{s}(s_{2}^{'})=p_{s}(\frac{5}{7})=p_{r}(r_{2})=0.21$

  $p_{s}(s_{3}^{'})=p_{s}(\frac{6}{7})=p_{r}(r_{3})+p_{r}(r_{4})=0.16+0.08=0.24$

  $p_{s}(s_{4}^{'})=p_{s}(1)=p_{r}(r_{5})+p_{r}(r_{6})+p_{r}(r_{7})=0.06+0.03+0.02=0.11$