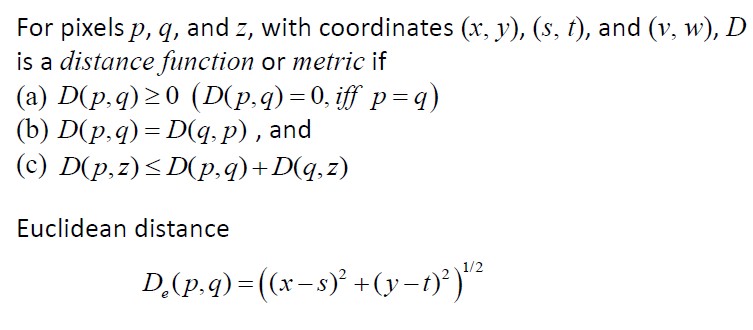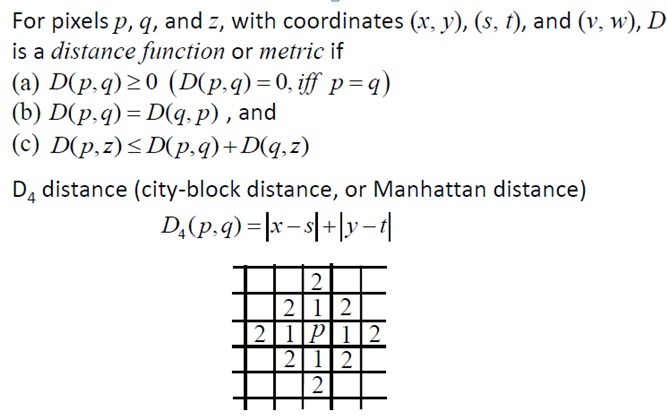1. 图像处理基础

1.1. 视觉感知的元素

人的眼镜结构
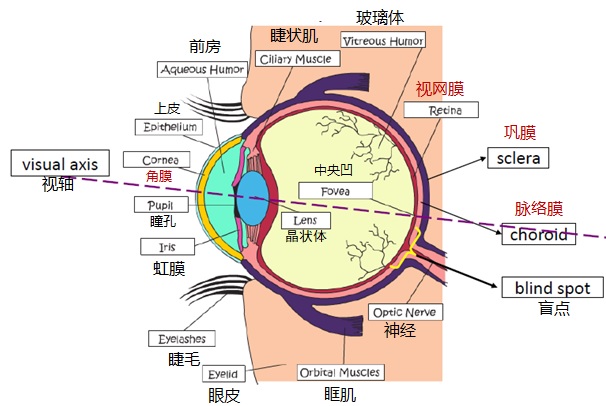
- 三层薄膜包围着眼睛：分别是眼角膜和巩膜外壳,脉络膜(choroid), 视网膜(retina)
- 脉络膜最前面分为睫状肌和虹膜。
- 脉络膜可以减少进入眼内的外来光和眼球内反向散射光的数量。
当眼球适当的聚焦时，来自眼睛外外部的光在视网膜上成像。
视网膜表面分布的分离光接收器提供了图案视觉。这种光接收器分为两类：锥状体cones 和杆状体rods。
锥状体主要分布在视网膜的中间部分，称之为中间凹fovea,对颜色灵敏度很高。常称之为白昼视觉或者亮光视觉
杆状体一般分布在视网膜的表面，杆状体用来给出视野外的一般的总体图像。他们没有色彩感觉，而在低照明度下对图像较敏感。常称之为夜视觉或暗视觉。
在神经区域，由于没有接收器而导致所谓的盲点blind spot。

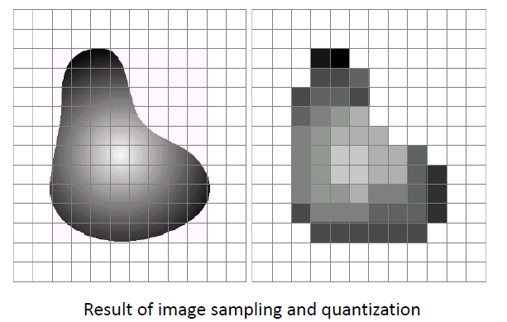
1.2. 图像采样和量化

采样和量化就是将连续的数字图像信号转化为离散的形式。
- 数字化坐标值叫作采样
- 数字化幅度值叫作量化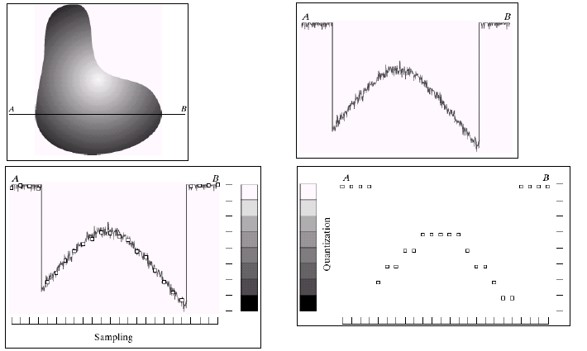

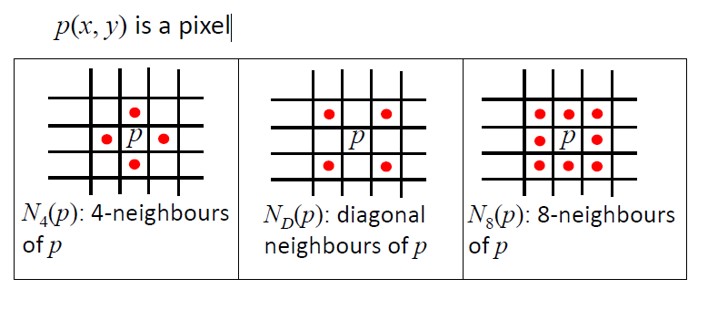
1.3. 像素间的基本关系

1.3.1. 像素间的邻接关系
- 欧式距离
- 曼哈顿距离

棋盘距离

1.4. 图像几何变换

问题的提出

在图像处理过程中，为了观测需要，常常需要对图像进行几何变换，如几何失真图像的校正、图像配准、电影、电视和媒体广告等的影像特技处理等，是图像变形以及校正变形的基础。
图像几何变换将图像中任一像素映射到一个新位置，是一种空间变换，关键在于确定图像中点与点之间的映射关系。
通过齐次坐标中，原图像进行平移、缩放、旋转等几何变换，可以用一个变换矩阵表示。
a,b,c,d用于图形的比例、对称、错切、旋转等基本变换；k,m用于图形的平移变换；p,q用于投影变换；s用于全比例变换。 $T = \left[\begin{matrix} a & b & k \\ c & d & m \\ p & q & s \end{matrix} \right]$
- 实现2D图像几何变换的基本变换的一般过程是
- 变换矩阵T×变换前的点集矩阵=变换后的点集矩阵

图像插值运算

指利用已知邻近像素点的灰度值来产生未知像素点的灰度值。
- 最近邻插值：非整数像素灰度值就等于距离最近的像素的灰度值。
- 双线性插值：利用非整数像素点周围的四个像素点的相关性，通过双线性算法计算得出的。 $\begin{matrix}f(x,y+b)=f(x,y) + b \times [f(x,y+1)-f(x,y)] \\ f(x+1,y+b) = f(x+1,y) + b \times [f(x+1,y+1)-f(x+1,y)]\\ f(x+a,y+b) = f(x,y+b)+a \times[f(x+1,y+b)-f(x,y+b)]\end{matrix}$
- 双三次插值：利用非整数像素点周围的16个像素点进行计算

图像几何变换步骤

根据不同的几何变换公式计算新图像的尺寸；
- 根据几何变换的逆变换，对新图像中的每一点确定其在原图像中的对应点；
- 按对应关系给新图像中各个像素赋值：
- 若新图像中像素点在原图像中的对应点坐标存在，直接赋值；
- 若新图像中像素点在原图像中的对应点坐标超出图像宽高范围，直接赋背景色；
- 若新图像中像素点在原图像中的对应点坐标在图像宽高范围内，采用插值的方法计算

图像的位置变换

图像的位置变换是指图像的大小和形状不发生变化，只是图像像素点的位置发生变化，含平移、镜像、旋转。
图像的位置变换主要是用于目标识别中的目标配准。

平移

$\begin{cases} x'=x+\Delta x \\ y'= y +\Delta y \end{cases}$

$\left[ \begin{matrix} x' \\ y' \\ 1 \end{matrix}\right] =\left[\begin{matrix}1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{matrix} \right]\left[\begin{matrix} x \\ y \\1 \end{matrix}\right]$

matlab函数

T = maketform(TRANSFORMTYPE,...)
B = imtransform(A,TFORM,INTERP,PARAM1,VAL1,PARAM2,VAL2,...)

Image=imread('lotus.jpg'); deltax=20; deltay=20;
T=maketform('affine',[1 0 0;0 1 0;deltax deltay 1]);
NewImage1=imtransform(Image,T,
                                             'XData',[1 size(Image,2)],
                                             'YData',[1,size(Image,1)],
                                             'FillValue',255);
NewImage2=imtransform(Image,T,
                                             'XData',[1 size(Image,2)+deltax],
                                             'YData',[1,size(Image,1)+deltay],
                                             'FillValue',255);
subplot(131),imshow(Image),title('原图');
subplot(132),imshow(NewImage1),title('画布尺寸不变平移');
subplot(133),imshow(NewImage2),title('画布尺寸扩大平移');

镜像

水平镜像 $\begin{cases} x'=M-1-x \\ y'=y\end{cases}$
垂直镜像 $\begin{cases}x'=x \\ y'=N-1-y\end{cases}$
对角镜像 $\begin{cases} x'= M-1-x \\ y' = N-1-y \end{cases}$

matlab函数

Image2=imread('lotus.jpg');   
         subplot(221),imshow(Image2);
HImage=flipdim(Image2,2); 
         subplot(222),imshow(HImage);
VImage=flipdim(Image2,1); 
         subplot(223),imshow(VImage);
CImage=flipdim(HImage,1); 
         subplot(224),imshow(CImage);

旋转

绕图像原点逆时针旋转 $\begin{cases} x = \rho cos \alpha \\ y = \rho sin \alpha\end{cases}$

$\begin{cases} x'=\rho cos(\alpha-\theta) \\ y'=\rho sin(\alpha - \theta)\end{cases} \rightarrow \begin{cases} x'=\rho cos \alpha \times cos \theta + \rho sin \alpha \times sin \theta = xcos\theta + y sin \theta \\ y'= \rho sin\alpha \times cos\theta - \rho cos\alpha \times sin \theta = -x sin\theta + y cos \theta\end{cases}$

绕原点旋转计算公式 $\begin{cases} x' = xcos\theta + y sin\theta \\ y'= -xsin\theta + ycos \theta\end{cases}$
旋转逆变换公式 $\begin{cases} x = x' cos\theta - y'sin\theta \\ y = x'sin\theta + y'cos\theta \end{cases}$

旋转变换过程
- 确定旋转后新图像尺寸,计算原图像四个角在旋转后的坐标

Image=im2double(imread('lotus.jpg'));
NewImage1=imrotate(Image,15);
NewImage2=imrotate(Image,15,'bilinear');
subplot(1,2,1),imshow(NewImage1);
subplot(1,2,2),imshow(NewImage2);

图像的形状变换

缩放

$\begin{cases} x'=k_{x}x \\ y'=k_{y}y\end{cases}$

M*N的图像缩小为 $k_{x}M \times k_{y}N$

错切

平面景物在投影平面上的非垂直投影，使图像中的图形产生扭变。 $\begin{cases} x' = x + d_{x}y \\ y'= d_{y}x +y\end{cases}$

$T = \left[\begin{matrix} 1 & d_{x} & 0 \\ d_{y} & 1 & 0 \\ 0 & 0 &1\end{matrix}\right]$

matlab程序

Image=im2double(imread(bird.jpg'));
tform1=maketform('affine',[1 0 0;0.5 1 0; 0 0 1]);
tform2=maketform('affine',[1 0.5 0;0 1 0; 0 0 1]);
NewImage1=imtransform(Image,tform1);
NewImage2=imtransform(Image,tform2);
subplot(1,2,1),imshow(NewImage1);
subplot(1,2,2),imshow(NewImage2);

1.5. 图像代数运算

加法运算

$g(x,y) = f_{1}(x,y) + f_{2}(x,y)$

和值处理
- 截断处理 $\begin{cases} g(x,y) = 255 & g(x,y)>255 \\ g(x,y) = g(x,y)& otherwise \end{cases}$
- 加权求和 $\begin{matrix}g(x,y) = \alpha \times f_{1}(x,y) +(1-\alpha)f_{2}(x,y) & \alpha \in [0,1] \end{matrix}$
- 主要应用
  - 多幅图像相加求平均去除叠加性噪声
  - 将一幅图像的内容经配准后叠加到另一幅图像上去，以改善图像的视觉效果。
  - 在多光谱图像中，通过加法运算加宽波段，如绿色波段和红色波段图像相加可以得到近似全色图像。
  - 用于图像合成和图像拼接。

matlab程序

Back=imread('desert.jpg');
Foreground=imread('car.jpg');
result1=imadd(Foreground,-100);
result2=imadd(Back,Foreground);
result3=imadd(Back,result1);
subplot(221),imshow(Foreground),title('原目标图');
subplot(222),imshow(result1),title('原目标图加标量');
subplot(223),imshow(result2),title('原目标图加背景');
subplot(224),imshow(result3),title('加标量图叠加背景');

减法运算

$g(x,y) = f_{1}(x,y) - f_{2}(x,y)$

差值处理
- 截断处理 $\begin{cases} g(x,y) = 0 & g(x,y)<0 \\ g(x,y) = g(x,y) & otherwise\end{cases}$
- 取绝对值 $g(x,y) = |f_{1}(x,y) - f_{2}(x,y)|$

主要应用
- 显示两幅图像的差异，检测同一场景两幅图像之间的变化
- 去除不需要的叠加性图案，加性图案可能是缓慢变化的背景阴影或周期性的噪声，或在图像上每一个像素处均已知的附加污染等。
- 图像分割：如分割运动的车辆，减法去掉静止部分，剩余的是运动元素和噪声。
- 生成合成图像。

matlab程序

Back=imread('hallback.bmp');
Foreground=imread('hallforeground.bmp');
result1=imabsdiff(Back,Foreground);
subplot(131),imshow(Back),title('背景图');
subplot(132),imshow(Foreground),title('前景图');
subplot(133),imshow(result1),title('图像相减');

乘法运算

$g(x,y) = f_{1}(x,y) \times f_{2}(x,y)$

主要应用
- 图像的局部显示和提取：用二值模板图像与原图像做乘法来实现。
- 生成合成图像
Matlab程序

Back=im2double(imread('bird.jpg'));
Templet=im2double(imread('birdtemplet.bmp'));
result1=immultiply(Templet,Back);
subplot(131),imshow(Back),title('背景');
subplot(132),imshow(Templet),title('模板');
subplot(133),imshow(result1),title('图像相乘');

除法运算

$g(x,y) = f_{1}(x,y) / f_{2}(x,y)$

主要应用

用于消除空间可变的量化敏感函数、归一化、产生比率图像等

matlab函数

Z = imdivide(X,Y)

1.6. 图像逻辑运算

非 $g(x,y) = 255 - f(x,y)$
与 $g(x,y) = f_{1}(x,y) \& f_{2}(x,y)$
或

$g(x,y) = f_{1}(x,y) | f_{2}(x,y)$

matlab函数

C = bitcmp(A) %按位求补
C = bitand(A,B)%按位求与
C = bitor(A,B) %按位求或
C = bitxor(A,B)% 按位求异或
% &、|、~：按运算数据的值，不按位

Back=imread('bird.jpg');
Templet=imread('birdtemplet.bmp');
result1=bitcmp(Back);
result2=bitand(Templet,Back);
result3=bitor(Templet,Back);
result4=bitxor(Templet,Back);
subplot(221),imshow(result1),title('求反');
subplot(222),imshow(result2),title('相与');
subplot(223),imshow(result3),title('相或');
subplot(224),imshow(result4),title('异或');

图像处理基础

1. 图像处理基础

1.1. 视觉感知的元素

人的眼镜结构