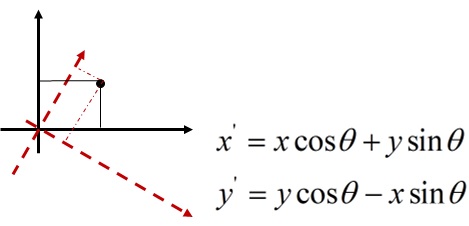1. 图像复原与重建

1.1. 图像复原

1.1.1. 周期噪声

  • 周期噪声是在图像获取中从电力或机电干扰中产生
  • 周期噪声可以通过频率域滤波显著减少 节点
function [f_noise] =  periodnoise(f,M,N,C)
% 正弦周期噪声
% f:原图像矩阵
% M,N：表示图像的行数和列数
% C：打扰因子
f_noise = f;
for i = 1 : M
    for j =1:N
    f_noise(i,j) = f(i,j) +C*sin(C*j) + C*sin(C*i);
    end
end

# Generating period noise 
f =imread('../pic/4.jpg'); 
[M,N] = size(f);
C = 40;  # 周期噪声幅度
f_noise= periodnoise(f,M,N,C);
figure;
subplot(221);
imshow(f);
title('原图像');
subplot(222);
imshow(f_noise);
title('添加周期噪声图像(C = 40)');
f1= fft2(double(f(:,:,1)));
f2 = fft2(double(f_noise(:,:,1)));
f1 = 1.0*log10(1+f1);
f2 = 1.0*log10(1+f2);
f1_1 = abs(fftshift(f1));
f2_1=abs(fftshift(f2));
subplot(223);imshow(f1_1,[]),title('频率域原图像');
subplot(224);imshow(f2_1,[]);title('频率域周期噪声污染的图像');

节点

1.1.2. 图像复原的频率域滤波器

  • 带阻滤波器

    • 阻止一定频率范围内的信号通过而允许其它频率范围内的信号通过，消除或衰减傅里叶变换原点处的频段

    • 理想带阻滤波器 H(u,v)={1D(u,v)<D0−W20D0≤D(u,v)≤D0+W21D(u,v)>D0+W2 H(u,v)=\biggr\{\begin{matrix} 1 & D(u,v) < D_{0}-\frac{W}{2} \\ 0 & D_0 \le D(u,v) \le D_{0}+\frac{W}{2} \\ 1 & D(u,v) \gt D_{0} +\frac{W}{2} \end{matrix}

      D(u,v)=(u−M2)2+(v−N2)2 D(u,v) = \sqrt{(u-\frac{M}{2})^2 +(v-\frac{N}{2})^2}

      • WW 是频带的宽带，D0D_{0}是频带的中心半径。
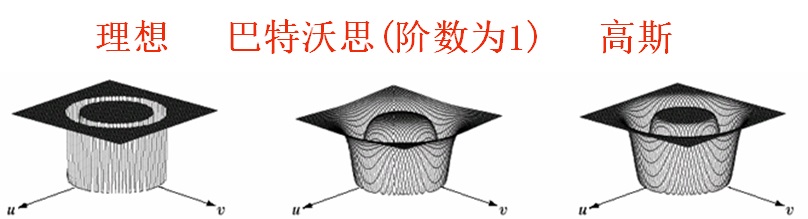
    • 巴特沃思带阻滤波器 H(u,v)=1(1+D(u,v)WD2(u,v)−D02)2n H(u,v) = \frac{1}{(1+\frac{D(u,v)W}{D^2(u,v)-D_{0}^{2}})^{2n}}

    • 高斯带阻滤波器 H(u,v)=1−e−12[D2(u,v)−D02D(u,v)W]2 H(u,v) = 1- e^{-\frac{1}{2}\biggr[\frac{D^2(u,v)-D_{0}^2}{D(u,v)W}\biggr]^2} 节点

      79

  • 带通滤波器

    • 允许一定频率范围内的信号通过而阻止其它频率范围内的信号通过。 Hbp=1−Hbr(u,v) H_{bp} = 1 -H_{br}(u,v)
    • Hbp(u,v)H_{bp}(u,v) 表示带通滤波器
    • Hbr(u,v)H_{br}(u,v) 表示带阻滤波器

  • 陷波滤波器

    • 阻止或通过事先定义的中心频率邻域内的频率
    • 由于傅里叶变换是对称的，陷波滤波器必须以关于原点对称的形式出现
    • 如果陷波滤波器位于原点处，则以它本身形式出现

  • 陷波带通滤波器：通过包含在陷波区的频率 Hnp(u,v)=1−Hnr(u,v) H_{np}(u,v) = 1 - H_{nr}(u,v)

    • Hnp(u,v)H_{np}(u,v)是陷波带通滤波器, Hnr(u,v)H_{nr}(u,v)对应的陷波带阻滤波器。
    • 当u0=v0=0u_{0}=v_{0}=0时，陷波带通滤波器变为低通滤波器 80

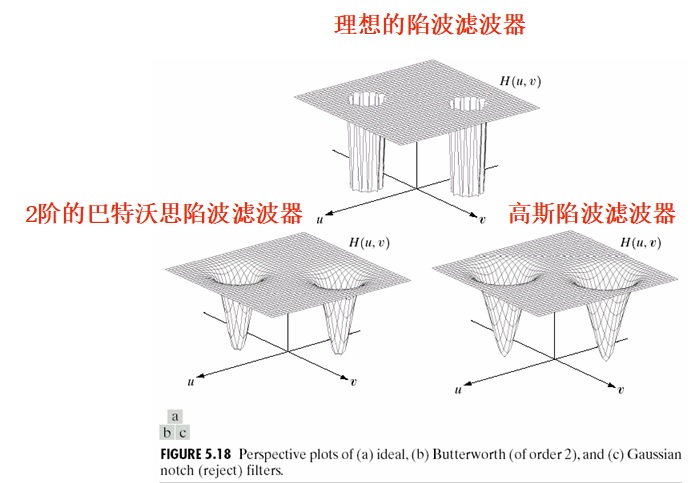
  • 理想陷波带阻滤波器 H(u,v)={0D1(u,v)orD2(u,v)≤D01otherwise H(u,v) = \biggr\{\begin{matrix} 0 & D_{1}(u,v) \quad or \quad D_{2}(u,v) \le D_{0} \\ 1 & otherwise \end{matrix} D1(u,v)=(u−M2−u0)2+(v−N2−v0)2 D_{1}(u,v) = \sqrt{(u-\frac{M}{2}-u_{0})^{2}+(v-\frac{N}{2}-v_{0})^{2}} D2(u,v)=(u−M2+u0)2+(v−N2+v0)2 D_{2}(u,v) = \sqrt{(u-\frac{M}{2}+u_{0})^{2}+(v-\frac{N}{2}+v_{0})^{2}}

    • 中心在(u0,v0)(u_{0},v_{0})且在(−u0,−v0)(-u_{0},-v_{0})对称

  • 巴特沃思陷波带阻滤波器 H(u,v)=11+[D02D1(u,v)D2(u,v)]2n H(u,v) = \frac{1}{1+\biggr[\frac{D_{0}^{2}}{D_{1}(u,v)D_{2}(u,v)}\biggr]^{2n}}

  • 高斯陷波带阻滤波器 H(u,v)=1−e−12[D1(u,v)D2(u,v)D02] H(u,v) = 1- e^{-\frac{1}{2}\biggr[\frac{D_{1}(u,v)D_{2}(u,v)}{D_{0}^{2}}\biggr]}

    • 注：当u0=v0=0u_{0}=v_{0}=0,上述3个滤波器变成高通滤波器
  • 陷波带通滤波器：通过包含在陷波区的频率 Hnp(u,v)=1−Hnr(u,v)H_{np}(u,v) = 1- H_{nr}(u,v)
    • Hnp(u,v)H_{np}(u,v)是陷波带通滤波器,Hnr(u,v)H_{nr}(u,v)对应的陷波带阻滤波器。
    • 当u0=v0=0u_{0}=v_{0}=0时，陷波带通滤波器变为低通滤波器

1.1.3. 图像退化

  • 在图像生成、记录、传输过程中，由于成像系统、设备或外在的干扰，会导致图像质量下降，称为图像退化，如大气扰动效应、光学系统的像差、物体运动造成的模糊、几何失真等。
  • 对退化图像进行处理，使之恢复原貌的技术称之为图像复原（Image Restoration）
  • 图像复原的关键在于确定退化的相关知识，将退化过程模型化，采用相反的过程尽可能恢复原图，或者说使复原后的图像尽可能接近原图。

  • 退化过程 81

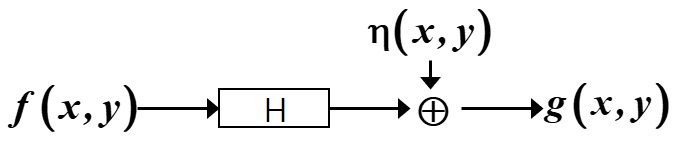
    • 抽象为一个退化系统H以及加性噪声的影响 g(x,y)=H[f(x,y)]+η(x,y) g(x,y) = H\biggr[f(x,y)\biggr]+\eta(x,y)

    • 用线性、空间不变系统模型来模拟实际中的非线性和空间变化模型 H[f(x,y)]=f(x,y)⋅h(x,y)=∫−∞+∞∫−∞+∞f(α,β)⋅h(x−α,y−β)dαdβ H[f(x,y)] = f(x,y)\cdot h(x,y) = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(\alpha,\beta)\cdot h(x-\alpha,y-\beta) d\alpha d\beta

    • 连续退化模型 g(x,y)=f(x,y)⋅h(x,y)+η(x,y) g(x,y) = f(x,y) \cdot h(x,y) + \eta(x,y)

      • h(x,y)h(x,y) 称为点扩散函数(PSF)，其傅里叶变换 H(x,y)H(x,y) 也称为光学传递函数(OTF)

    • 离散退化模型

      • f(α,β)f(\alpha,\beta),h(x−α,y−β)h(x-\alpha,y-\beta)进行均匀取样得到离散退化模型。

      • 采样延拓

        fe(x,y)={f(x,y)0≤x≤A−10≤y≤B−10A≤x≤M−1B≤y≤N−1 f_{e}(x,y) = \biggr\{\begin{matrix}f(x,y) & 0\le x \le A-1 \quad 0 \le y \le B-1 \\ 0 & A\le x \le M-1 \quad B \le y \le N-1\end{matrix}

        he(x,y)={h(x,y)0≤x≤C−10≤y≤D−10C≤x≤M−1D≤y≤N−1 h_{e}(x,y) = \biggr\{\begin{matrix}h(x,y) & 0 \le x \le C-1 \quad 0 \le y \le D-1 \\ 0 & C \le x \le M-1 \quad D \le y \le N-1\end{matrix}

      • 二维离散卷积退化模型

        ge(x,y)=∑m=0M−1∑n=0N−1fe(m,n)he(x−m,y−n) g_{e}(x,y) = \sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f_{e}(m,n)h_{e}(x-m,y-n)

      • 图像复原是指在给定退化图像g(x,y)g(x,y),了解退化的点扩散函数f(x,y)f(x,y)和噪声项η(x,y)\eta(x,y)的情况下，估计出原始图像。

  • 退化函数的步骤
    • 确定图像的退化函数
      • 退化函数一般是不知道的，需先估计退化函数
    • 采用合适的图像复原方法复原图像
      • 采用与退化相反的过程，使复原后的图像尽可能接近原图，一般要确定一个合适的准则函数，最优情况对应最好的复原图。这一步的关键技术在于确定准则函数和求最优
    • 可采用盲复原方法：直接从退化图像估计原图像

1.1.4. 基于模型的估计法

  • 若已知引起退化的原因，根据基本原理推导出其退化模型，称为基于模型的估计法

1.1.5. 运动模糊退化估计

  • 运动模糊图像

    • 景物和摄像机之间的相对运动，曝光时间内，景物在不同时刻产生多个影像，叠加而导致的模糊，称为运动模糊
      g(x,y)=∫0Tf(x−x0(t),y−y0(t))dt g(x,y) = \int_{0}^{T}f(x-x_{0}(t),y-y_{0}(t))dt

    • $x{0}(t)$,$y{0}(t)$ 为x、y方向上的运动分量，T为曝光时间

  • 运动模糊传递函数

    H(u,v)=∫0Te−j2π[uatT+vbtT]dt H(u,v) = \int_{0}^{T}e^{-j2\pi[\frac{uat}{T}+\frac{vbt}{T}]}dt

    H(u,v)=Tπ(ua+vb)]sin[π(ua+vb)]e−j2π(ua+vb) H(u,v) = \frac{T}{\pi(ua+vb)]}sin[\pi(ua+vb)]e^{-j2\pi(ua+vb)}

    • 匀速直线运动，T时间内，x、y方向上运动a和b

  • 运动模糊退化估计

    • 运动模糊的点扩散函数

      • 景物在x-y平面沿θ方向做匀速直线运动（θ是运动方向和x轴夹角），移动L个像素，点扩散函数为

      h(x,y)={1Ly=xtanθ,0≤x≤Lcosθ0y≠xtanθ,−∞<x<∞ h(x,y)=\biggr\{\begin{matrix}\frac{1}{L} & y = x\tan\theta, 0 \le x \le L\cos\theta\\ 0 & y \neq x \tan\theta, -\infty \lt x \lt \infty \\ \end{matrix}

    82

  %用MATLAB程序实现由于运动造成的图像模糊的实例
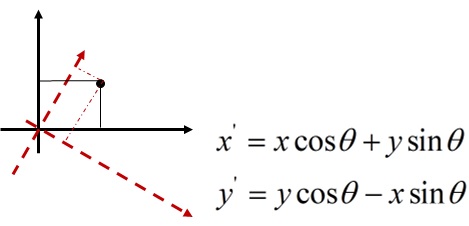
  I=imread('1.jpg');   %读取图片
  figure(1);
  subplot(221);
  imshow(I);
  %设置运动位移为30个像素
  LEN=30;
  %设置运动角度为75度
  THETA=75;
  %建立二维仿真线性运动滤波器PSF
  PSF=fspecial('motion',LEN,THETA);
  %用PSF产生退化图像
  MF=imfilter(I,PSF,'circular','conv');
  subplot(222);;imshow(MF);
  %运动模糊的图像
  wnr=deconvwnr(MF,PSF);
  subplot(223);;imshow(wnr);

83

  • 运动模糊点扩散函数参数估计
    • 基于频域特征的参数估计
    • 分析不同方向的运动模糊图像频谱变化 84

1.2. 图像重建

1.2.1. Radon变换

  • Radon是奥地利数学家(1887~1956) 85
  • 1917年发现了Rodon变换及其逆变换,但仅限于理论研究，没有实际应用
  • 科马克<美>和豪斯菲尔德<英>应用到CT领域
    • 发明第一台医学CT机
    • 获得了1979年诺贝尔医学奖

  • Radon变换的应用

    • CT (计算机断层扫描Computer Tomography)
    • MRI (磁共振成像Magnetic Resonance Imaging)
    • PET (正电子发射断层摄影术Positron Emission Tomography)
    • SPECT(单光子发射计算机断层成像Single Photon Emission Computer Tomography) 86

    • 直线L:

      ρ=xcos(θ)+ysin(θ) \rho = x\cos(\theta) + y\sin(\theta)

    • 将函数f(x,y)沿直线L做线积分

      R(ρ,θ)=∫Lf(x,y)ds R(\rho,\theta) = \int_{L}f(x,y)ds

    • 采用Δ\Delta函数表示直线L

      Δ(xcosθ+ysinθ−ρ)={0xcosθ+sinθ−ρ≠01xcosθ+sinθ−ρ=0 \Delta(x\cos\theta + y \sin \theta - \rho)=\biggr\{\begin{matrix} 0 & x\cos\theta + \sin\theta - \rho \neq 0 \\ 1 & x\cos\theta + \sin\theta - \rho =0 \end{matrix}

    • Randon变换对

      R(ρ,θ)=∫−∞+∞∫−∞∞f(x,y)Δ(xcosθ+ysinθ−ρ)dxdy R(\rho,\theta) = \int_{-\infty}^{+\infty}\int_{-\infty}^{\infty}f(x,y)\Delta(x\cos\theta + y \sin\theta - \rho)dxdy

      f(x,y)=12π2∫0πdθ∫−∞∞∂R/∂ρxcosθ+ysinθ−ρdρ f(x,y) = \frac{1}{2\pi^2}\int_{0}^{\pi}d\theta \int_{-\infty}^{\infty}\frac{\partial R / \partial \rho}{x\cos\theta + y \sin\theta - \rho}d\rho

    • 对一幅图像，在某一特定角度下的Radon变换会产生n个线积分值，构成一个n维的向量，称为f(x,y)在角度θ下的投影 87

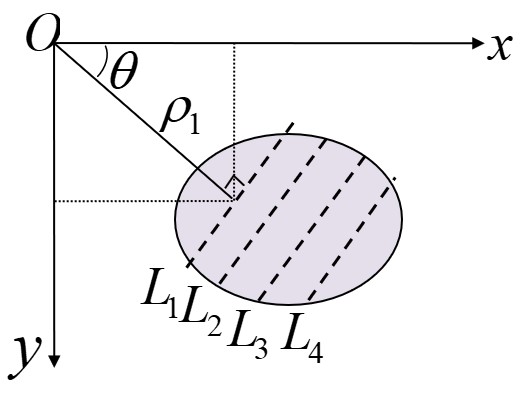
    • Radon变换即XY空间向ρθ空间的投影,ρθ空间每一点对应XY空间一条线

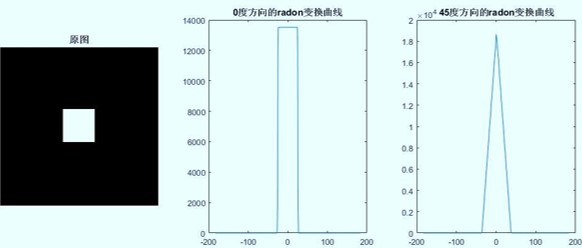
    • 例1：对图像进行指定方向上的Radon变换

          Image=rgb2gray(imread('block.bmp'));
    [R1,X1]=radon(Image,0);
    [R2,X2]=radon(Image,45);
    subplot(131),imshow(Image),title('原图');
    subplot(132),plot(X1,R1),title('0°方向上的Radon变换');
    subplot(133),plot(X2,R2),title('45°方向上的Radon变换');

      88

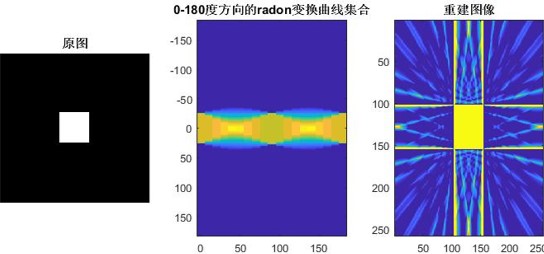
    • 例2：对图像进行Radon变换和反变换

        Image=rgb2gray(imread('block.bmp'));
  theta=0:10:180;
  [R,X]=radon(Image,theta);   
  result=iradon(R,theta);
  subplot(131),imshow(Image),title('原图');
  subplot(132),imagesc(theta,X,R),
  title('radon变换曲线集合');
  subplot(133),image(result),
  title('重建图像');

      89

  • Radon变换的应用
    • 可用来检测图像中的线段
      • 图像中高灰度值的线段在ρθ空间形成亮点，低灰度值的线段形成暗点，对图像中线段的检测可转化为在ρθ空间对亮点、暗点的检测
    • 计算出原图中各方向上的投影值，可以作为方向特征用于目标检测和识别
    • 改变图像的表现形式，为相关处理提供便利
Copyright © ZHOUWEN all right reserved，powered by GitbookLatest updated： 2022-05-01 16:20:46

results matching ""

    No results matching ""