1. 小波变换

1.1. 背景

• 传统的信号理论，是建立在傅里叶分析基础上的，而傅里叶变换作为一种全局性的变化，其有一定的局限性
  • 具有不规则特征（比如峰值等）的非周期信号就不是那么管用了。不幸的是，大部分现实生活的现象中，从说话的声音到地震数据，都属于非周期类别
• 20世纪70年代，在法国石油公司工作的年轻的地球物理学家Jean Morlet提出了小波变换(wavelet transform , WT)的概念
• 20世纪80年代，开发了连续小波变换(continuous wavelet transform , CWT)
• 法国科学家Meyer创造性地构造出具有一定衰减性的光滑函数，用于分析函数用缩放与平移均为$2^j$ (j≥0的整数)的倍数构造了L2(R)空间的规范正交基，使得小波分析得到发展
• 频域成分相同的信号，即使信号在时域上的分布不一样，FFT变换后的频域图却几乎完全一样
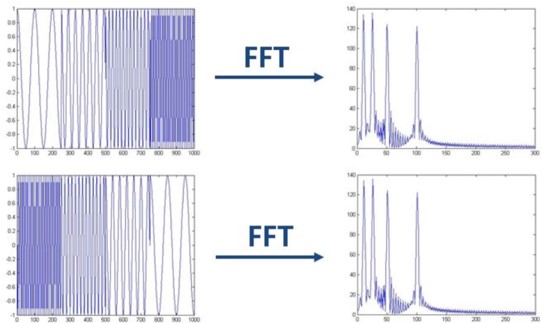
  • 傅里叶变换只可以获得一幅图像总体上包含哪些成分，但是对各成分出现的时间并无所知。
  • 时域相差很大的图像，FFT之后的频域图可能完全相同
• 小波变换更换傅里叶变换的基
  • 将无限长的三角函数基换成了有限长的会衰减的小波基，这样不仅可以获取频率，还可以定位到时间
  • 传统的傅里叶分析中，信号是完全在频域展开，不包含任何时域信息。而小波变换具有多分辨率的特点，在时域和频域上都有表征局部信息的能力，时间窗和频率窗都可以根据信号的具体形态动态调整
  • 在低频部分采用较低的时间分辨率，提高频率的分辨率
  • 在高频情况下，采用较低的频率分辨率来获得精确的时间定位。
  • 小波变换被广泛地应用在诸多领域，在信号分析方面主要用于滤波、去噪、压缩和传递等方面

1.2. 小波

• 定义
  • 设函数$\psi(t)$满足:$\int_{R}\psi(t)dt$,对其进行平移和伸缩产生函数族:$\psi_{a,b}(t)=\frac{1}{\sqrt{a}}\psi(\frac{t-b}{a})$, $a,b\in R,a \ne 0$. $\psi(t)$ 称为基小波或母小波，a为伸缩因子（尺度因子）,b为平移因子， $\psi_{a,b}(t)$为$\psi(t)$生成的连续小波。

1.3. 小波函数

• 如果函数能在有限的区域内迅速衰减到0，这样的函数称为母小波，由它生成的一组正交基称为小波函数

• 如果$\phi(t)\in L^2(R)$满足以下条件： $C_{\phi}= \int _{-\infty}^{+\infty}(\frac{|\hat\phi(\omega)|}{|\omega|})d\omega \lt \infty$

  • 那么$\phi(t)$称为基小波，其中 $\hat\phi(t)$ 是 $\phi(t)$的傅里叶变换

  • 由基小波生成的小波函数可表示：

    $\phi_{a,b}(t) = \frac{1}{\sqrt{|a|}}\phi(\frac{t-b}{a})$

• 连续小波变换

  • 设$f(t)\in L^2(R)$,则对其的连续小波变换为： $(W_{\phi}f)(a,b) = \int_{-\infty}^{+\infty}f(t)\overline {\phi_{a,b}(t)}dt$

• 离散小波变换

  • 离散小波函数表示为： $\phi_{j,k}(t) = a_{0}^{-\frac{j}{2}}\phi(a_{0}^{-j}t - kb_{0}),j,k\in Z$
  • 离散小波变换的系数表示为:
    • 其中C为与信号无关的常数，如果取$a_0=2$,$b_0=1$,则称二进制小波变换 $f(t) = C\sum_{-\infty}^{+\infty}\sum_{-\infty}^{+\infty}W_{j,k}\phi_{j,k}(t)$

• 正交小波变换

  • 设${\phi_{j,n}(x)}_{j,n \in Z}$ 是 $L^{2}(R)$ 的标准化正交基，由于对于 $\forall f \in L^{2}(R)$, 都有 $f(x)= \sum_{j,n\in Z}<f,\phi_{j,n}>\phi_{j,n}(x)$
  • 小波函数
    • Harr小波 $\Psi_{H}(x)=\left\{\begin{matrix}1 & 0\le x \le 0.5 \\ -1 & 0.5 \le x \le 1 \\ 0 & otherwise \end{matrix} \right.$
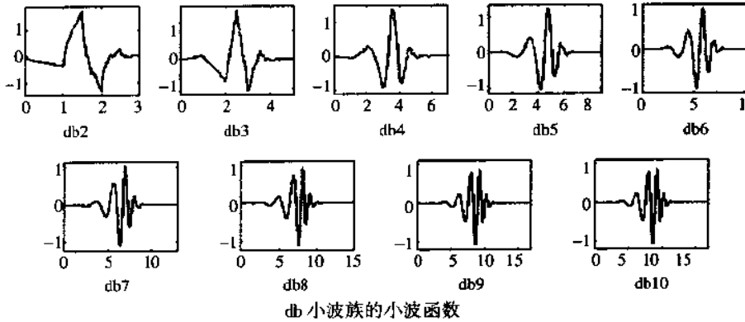
    • Daubechies小波，db1小波等同于Haar小波，其余小波没有解析的表达式

1.4. 小波变换

• 一级二维离散小波变换

  [CA,CH,CV,CD]=dwt2(X,’wname’) 或 [CA,CH,CV,CD]=dwt2(X, Lo_D, Hi_D)
  

• 一级二维离散小波逆变换

  X=idwt2(CA,CH,CV,CD,’wname’) 或X=idwt2(CA,CH,CV,CD, Lo_D, Hi_D)
  

• 多级二维小波分解

      [C,S] = wavedec2(X,N,'wname') 或
      [C,S] = wavedec2(X,N,Lo_D,Hi_D)