1. MATLAB绘图与可视化
MATLAB中有大量函数和命令来绘制出各种各样的图形,具有强大的绘图功能



···
1.1. 概述
使用MATLAB绘制二维曲线,特殊二维图形,三维曲线及曲面,以及曲线和图形修饰等内容。
1 准备作图数据(必须)
(1) 使用load命令调入.txt数据(\<=txt);
(2) 通过系统函数/用户自编函数得到作图数据(\<=m);
(3) 直接输入命令(\<=命令窗口)。
(4) 在主工作窗口,导入可以识别的数据文件。
2 选定作图窗口与作图区域
figure函数指定绘图窗口, subplot函数指定当前图形窗口的绘图子区域。
3 调入作图函数命令(必须) plot
4 设置图形格式
线形、颜色、数据点标记、坐标轴、标题、网格线、图例和文本修饰等
5 输出所制作的图形
可以将绘制的图形窗口保存为.fig文件,或者转换为别的图形文件,也可以复制图片,或者打印图片等。
其中步骤1和步骤3是必不可少的绘图步骤,其他步骤系统通常都有相应的默认设置,可以省略。例如,要在[0,2]内,绘制正弦函数的图形,可以用下面简单的语句:
t=0:0.1:2*pi;
y=sin(t);
plot(t,y)
其中前两个语句是步骤1准备绘图数据,plot函数是步骤3,调用绘图函数画图。

1.2. 二维曲线的绘制
1.2.1. 绘图基本函数
plot函数可以在二维平面上绘制不同的曲线,它有下列几种用法
1. plot(y)
功能:绘制以y为纵坐标的二维曲线
说明:
(1)当y为长度为n的向量时,则纵坐标为y,横坐标MATLAB根据y向量的元素序号自动生成,为1:n的向量。
(2)当y为矩阵时,plot(y)的功能是将矩阵的每一列画一条曲线,共n条曲线,每个曲线自动用不同颜色表示,每条曲线横坐标为向量1:m,m为矩阵的行数。
例如,绘制幅值为1的锯齿波。
程序代码如下,结果如右图所示。
>> y=[0 1 0 1 0 1 0 1 0]
y = 0 1 0 1 0 1 0 1 0
>> plot(y)
2. plot(x, y)
功能:绘制以x为横坐标,y为纵坐标的二维曲线
说明:
(1)x和y为向量时的plot(x, y)当x和y都是向量时,它们长度必须相等,正弦曲线就是这种情况。
(2)x为向量y为矩阵时的plot(x, y)要求x的长度必须和y的行数或者列数必须相等。当向量x的长度和矩阵y的行数相等,向量x和y的每一列向量画一条曲线;当向量x的长度与矩阵y的列数相等时,则向量x和y的每一行向量画一条曲线;如果y是方阵,则向量x与矩阵y的每一列向量画一条曲线。
(3)x是矩阵y是向量时,要求x的行或列数必须和y的长度相等。与(2)相似。
(4)x和y都是矩阵时,要求x和y大小必须相等,矩阵x的每一列与y对应的每一列画一条曲线。
例如,用plot绘制幅值为1,周期为2s的方波。
>>x=[0 1 1 2 2 3 3 4 4 5 5];
>> y=[1 1 0 0 1 1 0 0 1 1 0];
>> plot(x,y)
>> axis([0 6 0 1.5])
3. plot(x1,y1,x2,y2,…)
功能:在同一坐标轴下绘制多条二维曲线。
plot(x1,y1,x2,y2,…)函数可以在一个图形窗口同一坐标轴下绘制多条曲线,MATLAB自动以不同颜色绘制不同曲线。
【例】在一个图形窗口同一坐标轴绘制sin(x),cos(x), ,
四种不同的曲线。
程序代码如下,结果如下图所示。
x=0:0.1:2*pi;
y1=sin(x);
y2=cos(x);
y3=sin(x).^2;
y4=cos(x).^2;
plot(x,y1,x,y2,x,y3,x,y4)
1.2.2. 线性图格式设置
1.设置曲线的线型、颜色和数据点标记
为了便于曲线比较,MATLAB提供一些绘图选项,可以控制所绘的曲线的线型、颜色和数据点的标识符号。命令格式如下:
plot(x, y,’选项’)
其中,选项具体定义见表所示。当选项省略时,MATLAB默认线型一律使用实线,颜色将根据曲线的先后顺序依次采用下表给出的颜色。
| 颜色 | 线型 | 数据点标识 | |||
|---|---|---|---|---|---|
| 类型 | 符号 | 类型 | 符号 | 类型 | 符号 |
| 蓝色 | b(blue) | 实线(默认) | - | 实点标记 | . |
| 绿色 | g(green) | 点线 | : | 圆圈标记 | o |
| 红色 | r(red) | 虚线 | -- | 叉号标记 | x |
| 青色 | c(cyan) | 点画线 | -. | 十字标记 | + |
| 紫红色 | m(magenta) | 星号标记 | * | ||
| 黄色 | y(yellow) | 方块标记 | s | ||
| 黑色 | k(black) | 钻石标记 | d | ||
| 白色 | w(white) | 向下三角标记 | v | ||
| 向上三角标记 | \^ | ||||
| 向左三角标记 | \< | ||||
| 向右三角标记 | > | ||||
| 五角星标记 | p | ||||
| 六角形标记 | h |
【例】在一个图形窗口同一坐标轴绘制,绘制蓝色、实线和数据点标记为圆圈的正弦曲线,同时绘制红色,点画线,数据点为钻石标记余弦曲线。
程序代码如下,结果如下图所示。
clear
x=0:0.1:2*pi;
y1=sin(x); y2=cos(x);
plot(x,y1,'b-o',x,y2,'r-.d')
2.设置坐标轴
MATLAB可以通过函数设置坐标轴的刻度和范围来调整坐标轴。设置坐标轴函数axis的常用调用格式如下表所示。
| 函数命令 | 功能及说明 | 函数命令 | 功能及说明 |
|---|---|---|---|
| axis auto | 使用默认设置 | axis manual | 保持当前坐标范围不变 |
| axis([xmin,xmax, ymin,ymax]) | 设定坐标范围,且要求xmin\<xmax,ymin\<ymax | axis fill | 在manual方式下,使坐标充满整个绘图区域 |
| axis equal | 横纵坐标使用等长刻度 | axis on | 显示坐标轴 |
| axis square | 采用正方形坐标系 | axis off | 取消坐标轴 |
| axis normal | 默认矩形坐标系 | axis xy | 普通直角坐标,原点在左下方 |
| axis tight | 把数据范围设为坐标范围 | axis ij | 矩阵式坐标,原点在左上方 |
| axis image | 横纵轴采用等长刻度,且坐标框紧贴数据范围 | axis vis3d | 保持高宽比不变,三维旋转时避免图形大小变化 |
【例】使用调整坐标轴函数axis,实现sin(x)和cos(x)两条曲线的坐标轴调整。
程序代码如下所示。
x=0:0.1:2*pi; y1=sin(x); y2=cos(x);
plot(x,y1,x,y2) ;axis([0 4*pi -2 2]) %设置横纵坐标为[0,4],[-2,2]
figure;plot(x,y1,x,y2);axis([0 pi 0 0.9]) %设置横纵坐标为[0,],[0,0.9]
figure;plot(x,y1,x,y2);axis image %设置横纵轴等长,坐标框紧贴数据范围
figure;plot(x,y1,x,y2);axis tight %设置数据范围设为坐标范围
3.网格线和坐标边框
(1)网格线
网格线是根据坐标轴的刻度使用虚线分隔。默认设置是不显示网格线。
MATLAB使用grid on函数显示网格线;grid off函数不显示网格线;反复使用grid函数可以在grid on和grid off之间切换。
(2)坐标边框
坐标边框是指坐标系的刻度框,MATLAB使用box on函数实现添加坐标边框;box off函数去掉当前坐标边框;反复使用box函数则在box on和box off之间切换。默认设置是添加坐标边框。
【例】绘制曲线及包络线,使用网格线函数grid分别实现在坐标轴上添加和不显示网格线;利用三维表面图函数surf绘制peaks曲面图,利用坐标边框函数box,添加和不显示坐标边框功能。
程序代码如下,结果如图所示。
Close all
x=(0:0.1:2*pi)';
y1=3*exp(-0.3*x)*[1,-1];
y2=3*exp(-0.3*x).*sin(2*x);
plot(x,y1,x,y2)
figure;plot(x,y1,x,y2)
grid on
figure;plot(x,y1,x,y2)
[X,Y,Z] = peaks;
surf(X,Y,Z);box on
figure;[X,Y,Z] = peaks;
surf(X,Y,Z);box off
plot的调用格式
plot(x) —— 缺省自变量绘图格式,x为向量, 以x元素值为纵坐标,x的序号为横坐标绘图。
plot(x,y) —— 以x元素为横坐标值,y元素为纵坐标值绘制曲线。x,y均为向量时,要求长度一致;
plot(x1,y1,’参数1‘,x2,y2,’参数2‘…) —— 多条曲线绘图格式,以公共的x元素为横坐标值,以y1,y2…元素为纵坐标值,根据确定的参数绘制曲线。
x=0:pi/10:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2);
plot(x,y1,'r+-',x,y2,'k*:')

1.2.3. 图形修饰
MATLAB提供很多图形修饰函数,实现对图形添加标题(title)、横纵坐标轴的标签(label),图形某一部分文本标注(text),不同数据线的图例标识(legend)等功能。
1.标题和标签设置
MATLAB提供title函数和label函数实现添加图形的标题和坐标轴的标签功能。它们的调用格式为:
(1) title(’str’)
(2) xlabel (’str’ )
(3) ylabel (’str’)
(4)zlabel (’str’)
其中,title为设置图形标题的函数,xlabel、ylabel和zlabel为设置x、y和z坐标轴的标签函数。str为注释字符串,也可为结构数组。
2.图形的文本标注
MATLAB提供text和gtext函数,能在坐标系某一位置标注文本注释。
(1)text(x, y, ’str’)
(2)gtext(’str’)
(3)gtext({’str1’;’str2’;’str3’;…})
其中,text(x, y, ’str’)函数能在坐标系位置(x,y)处添加文本str注释;gtext(’str’)可以为鼠标选择的位置处添加文本str注释; gtext({’str1’;’str2’;’str3’;…})一次放置一个字符串多次放置在鼠标指定位置上。
【例】使用title,、xlabel、ylabel、text和gtext函数,对正弦曲线设置标题,横纵坐标轴标签,在曲线特殊点标识文本注释。
程序代码如下,结果如下图所示。
t=0:0.1:2*pi; y=sin(t);
plot(t,y)
xlabel('t(S)')
ylabel('sin(t)(V)')
grid on
title('This is an example of sin(t)\rightarrow 2\pi')
text(pi,sin(pi),'\leftarrow this is a zero point for\pi')
gtext('\uparrow this is a max point for\pi/2')
gtext('\downarrow this is a min point for 3*\pi/2')
3. 图例设置
为了区别在同一坐标系里多条曲线,一般会在图形空白处添加图例。MATLAB提供legend函数可以添加图例,函数调用格式为:
legend(’str1’,’str2’,…,’location’,LOC)
其中,str1,str2,…为图例标题,与图形内曲线依次对应。LOC为图例放置位置参数,LOC的取值如下表所示。legend off为删除当前图中的图例。
【例】在同一坐标系中,分别绘制以红实线,数据点标记为“*”的正弦曲线和绿点画线,数据点标记为“o”的余弦曲线,并设置适当的图例、标题和坐标轴标签。
t=0:0.1:2*pi; y1=sin(t); y2=cos(t);
plot(t,y1,'r-*',t,y2,'g-.o')
xlabel('t(S)')
ylabel('sin(t)&cos(t)(V)')
grid on
title('正弦和余弦曲线')
legend('正弦曲线','余弦曲线','location','north') %图例放在图内顶部
legend('正弦曲线','余弦曲线','location','best') %图例放在图内最佳位置
4.用鼠标获取二维图形数据
MATLAB提供ginput函数,实现用鼠标从图形获取数据功能。ginput函数在工程设计、数值优化中很有用,仅适用于二维图形。该函数格式如下:
[x, y]=ginput(n) %用鼠标从图形中获取n个点的坐标(x,y)
其中,n为正整数,是通过鼠标在图形中获取数据点的个数;x和y是用来存放所获取的坐标,是列向量,每次获取的坐标点位列向量一个元素。
当运行ginput函数后,会把当前图形从后台调到前台,同时鼠标光标变为十字叉,用户移动鼠标将十字叉移动到待取坐标点,单击鼠标左键,便获得该点坐标。当n个点的数据全部取完后,图形窗口便退回后台。
例如,在命令窗口中使用ginput函数,从图形窗口获取2点的坐标数据,存放在变量x和y中。
>> [x,y]=ginput(2)
1.2.4. 图形保持
【例】用图形保持功能在同一坐标内,绘制曲线 ,,及其包络线。
t=(0:0.1:2*pi)';
y1=3*exp(-0.3*t)*[1,-1];
y2=3*exp(-0.3*t).*sin(3*t);
plot(t,y1,'r:') %绘制包络线
hold on %打开图形保持功能
plot(t,y2,'b-') %绘制曲线y
legend('包络线','包络线','曲线y','location','best')
xlabel('t') %设置横坐标签
ylabel('y') %设置纵坐标签
hold off %关闭图形保持功能
grid on %添加网格线
1.2.5. 多个图形绘制
subplot函数可以在同一窗口分割成多个子图,能在不同坐标系绘制不同的图形。subplot函数的格式如下:
Subplot(m,n,p) %将图形窗口分割成()子图,在第p幅为当前图。
其中,subplot中的逗号“,”可以省略;子图排序:左上方为第一幅,从左往右,从上向下依次排序;m为子图行数,n为列数,共分割为个子图。
【例】试在同一图形窗口的四个子图中,用不同的坐标系绘图在的四条不同的曲线。
t=(0:0.1:2*pi);
y1=sin(t);y2=cos(t);
y3=sin(2*t);y4=cos(2*t);
subplot(2,2,1);plot(t,y1)
title('sin(t)')
subplot(2,2,2);plot(t,y2)
title('cos(t)')
subplot(2,2,3);plot(t,y3)
title('sin(2*t)')
subplot(2,2,4);plot(t,y4)
title('cos(2*t)')
1.3. 二维特殊图形的绘制
MATLAB使用bar,barh,bar3和bar3h函数来绘制柱状图,它们的调用格式如下:
(1)bar(x,y, width, 参数) %绘制垂直柱状图
其中x是横坐标向量,默认省略值为1:m,m为y的向量长度;y是纵坐标,可以是向量或者矩阵,当向量时,每个元素对应一个竖条,当的矩阵时,绘制m组竖条,每组包含n条;width是竖条的宽度,默认省略宽度为0.8,如果宽度大于1,则条与条之间将重叠;参数是控制条形显示效果,有’grouped’分组式和’stacked’堆栈式,默认省略为’grouped’。
1.3.1. 柱状图
MATLAB使用bar,barh,bar3和bar3h函数来绘制柱状图,它们的调用格式如下:
(2)barh(x, y, width, 参数) %绘制水平柱状图
其中,变量及参数定义与bar函数一致。
(3)bar3(x, y, width, 参数) %绘制三维垂直柱状图
(4)barh3(x, y, width, 参数) %绘制三维水平柱状图
其中bar3和barh3函数的变量的定义与bar类似;参数除了有’grouped’分组式和’stacked’堆栈式,多了’detached’分离式,默认为’detached’。
【例】已知某个班4位学生,在五次考试中取得下列成绩,如下表所示,请用垂直柱状图,水平柱状图,三维垂直柱状图和三维水平柱状图分别显示成绩。
| 学生 第几次 | 第一次考试 | 第二次考试 | 第三次考试 | 第四次考试 | 第五次考试 |
|---|---|---|---|---|---|
| 1 | 98 | 90 | 60 | 75 | 80 |
| 2 | 78 | 87 | 90 | 80 | 65 |
| 3 | 50 | 70 | 89 | 99 | 92 |
| 3 | 86 | 83 | 70 | 60 | 94 |
clear
x1=[98 90 60 75 80];
x2=[78 87 90 80 65];
x3=[50 70 89 99 92];
x4=[86 83 70 60 94];
x=[x1;x2;x3;x4];
subplot(2,2,1);bar(x)
title('垂直柱状图')
xlabel('学生');ylabel('分数')
subplot(2,2,2);barh(x,'stacked')
title('水平柱状图')
xlabel('分数');ylabel('学生')
subplot(2,2,3);bar3(x)
title('三维垂直柱状图')
xlabel('第几次考试');ylabel('学生');zlabel('分数')
subplot(2,2,4);bar3h(x,'detached')
title('三维水平柱状图')
xlabel('第几次考试');ylabel('分数');zlabel('学生')
1.3.2. 饼形图
MATLAB提供pie和pie3函数绘制二维和三维饼形图,它们的调用格式为:
(1) pie(x, explode, ’label’) %绘制二维饼图
其中,当x为向量时,每个元素占总和的百分比;当x为矩阵时候,每个元素占矩阵所有元素总和的百分比;explode是与x同长度的向量,用于控制是否从饼图中分离对应的一块,非零元素表示该部分需要分离,系统默认是省略explode项,即不分离;label是用来标注饼形图的字符串数组。
(2) pie3(x, explode, ’label’) %绘制三维饼图
其中,变量及参数定义和二维饼图pie函数一致。
【例】已知一个服装店四个月的销售数据为x=[210 240 180 300],分别用二维和三维饼图显示销售数据
clear
x=[210 240 180 300];
subplot(2,2,1);
pie(x,{'一月份','二月份','三月份','四月份'})
title('销售额的二维饼图')
subplot(2,2,2);
pie(x,[0 0 1 0])
title('销售额的二维饼图(分离)')
subplot(2,2,3);
pie3(x,{'一月份','二月份','三月份','四月份’})
title('销售额的三维饼图')
subplot(2,2,4);
pie3(x,[0 0 0 1],{'一月份','二月份','三月份','四月份’})
title('销售额的三维饼图(分离)')
1.3.3. 直方图
MATLAB提供hist函数用于绘制条形直方图。直方图的横坐标将数据范围划分成若干段,纵坐标显示每段数据个数。函数调用格式如下:
(1)hist(y,n) %统计每段元素个数并绘制直方图
(2)hist(y,x)
(3)N=hist(y,x)
其中,n为分段的个数,若n省略时,默认分成10段;x是向量,用于指定所划分每个数据段的中间值;y可以是向量,也可以是矩阵,如果是矩阵,则按列分段;N是每段元素的个数。
【例】用直方图hist函数,绘制rand(10000,1)和randn(10000,1)函数产生的数据的直方图。
y1=rand(10000,1);
y2=randn(10000,1);
subplot(2,2,1);hist(y1,50) %绘制均匀分布的直方图(50分段)
title('均匀分布的直方图(50分段)')
subplot(2,2,2);hist(y1,[0:0.1:1]) %绘制均匀分布的直方图(10分段)
title('均匀分布的直方图(10分段)')
subplot(2,2,3);hist(y2) %绘制正态分布的直方图(默认分段)
title('正态分布的直方图(默认段)')
subplot(2,2,4);hist(y2,[-5:0.1:5]) %绘制正态分布的直方图(100分段)
title('正态分布的直方图(100分段)')
N1=hist(y1,10) %统计10个分段,每段多少个元素
N2=hist(y2) %统计默认10分段,每段多少个元素
>>
N1 = 960 1017 1042 985 988 1048 971 1005 995 989
N2 = 6 64 377 1366 2607 3006 1803 647 115 9
验证了它们服从均匀分布和正态分布。
1.3.4. 离散数据图
1.stairs阶梯图
MATLAB提供stairs函数绘制阶梯图,stairs函数的调用格式如下:
stairs(x,y,’参数’)
其中,stairs函数的格式与plot函数相似,不同的是将数据用一个阶梯图表示, x是横坐标,当x省略时,横坐标为1:size(y,1);如果y是矩阵,则绘制每一行画一条阶梯曲线;参数主要是控制线的颜色和线型,和plot函数定义一样。
2.stem火柴杆图
MATLAB提供stem函数绘制火柴杆图,stem函数的调用格式如下:
Stem(x, y, ’参数’)
其中,stem函数绘制的方法和plot命令很相似,将数据用一个垂直的火柴杆表示,火柴头的小圆圈表示数据点;当x省略时,横坐标为1:size(y,1);y是用于画火柴杆的数据,若y是矩阵则每一行数据画一条火柴杆曲线;参数可以是’fill’或线型,’fill’表示将火柴头填充,线型与plot线型参数相似。
3. candle蜡烛图
MATLAB提供candle函数绘制蜡烛图,即股票的分析图,其调用格式如下:
candle(HI, LO, CL, OP)
其中,HI为股票的最高价格向量;LO 为股票的最低价格向量;CL 为股票的收盘价格向量;OP 为股票的开盘价格向量。
【例】使用stairs函数和stem函数绘制正弦离散数据y=sin(t)阶梯图和火柴杆图。
程序代码如下,结果如下图所示。
t=0:0.1:2*pi;y=sin(t);
subplot(2,1,1);stairs(t,y,'r-')
xlabel('t');ylabel('sin(t)')
title('正弦曲线的阶梯图')
subplot(2,1,2);stem(t,y,'fill')
xlabel('t');ylabel('sin(t)')
title('正弦曲线的火柴杆图')
【例】使用candle函数绘制2017年2月27日到3月14日,12个交易日大众公用股票的蜡烛图,即分析图。
程序代码如下,结果如下图所示。
open=[6.42 6.37 6.38 6.53 6.44 6.48 6.46 6.44 6.44 6.52 6.52 6.53]';
high=[6.55 6.42 6.68 6.60 6.49 6.49 6.49 6.54 6.66 6.55 6.58 6.55]';
low=[6.38 6.34 6.38 6.43 6.42 6.43 6.40 6.42 6.35 6.43 6.48 6.43]';
close=[6.38 6.39 6.55 6.46 6.46 6.47 6.46 6.46 6.56 6.50 6.53 6.45]';
candle(high,low,close,open)
xlabel('t');ylabel('股票价格')
title('大众公用2017.2.27至3月14日12个交易日趋势图')
1.3.5. 向量图
MATLAB提供三种绘制向量图的函数:罗盘图compass函数、羽毛图feather函数和向量场quiver函数。
1. 罗盘图
MATLAB提供compass函数绘制罗盘图,在极坐标系中绘制从原点到每一个数据点带箭头的线段。函数调用格式如下:
(1)compass(u,v,’线型’) %绘制横坐标为u,纵坐标为v的罗盘图
(2)compass(Z,’线型’) %绘制复向量Z的罗盘图
其中,u和v分别是复向量Z的实部和虚部,u=real(Z),v=imag(Z)
2. 羽毛图
MATLAB提供feather函数绘制羽毛图,在直角坐标系中绘制从原点到每一个数据点带箭头的线段。函数调用格式如下:
(1)feather(u,v,’线型’) %绘制横坐标为u,纵坐标为v的羽毛图
(2)feather(Z,’线型’) %绘制复向量Z的羽毛图
3. 向量场
MATLAB提供quiver函数绘制向量场图,在直角坐标系中绘制从(x,y)为起点,到每一个数据点带箭头的向量场。函数调用格式如下:
quiver(x, y, u, v) %绘制以(x,y)为起点,横纵坐标为(u,v)的向量场
【例】已知三个复数向量A1=5+5i,A2=3-4i和A3=-4+2i,使用compass、feather和quiver函数绘制复向量的向量图。
程序代码如下,结果如下图所示。
A1=5+5i;A2=3-4i; A3=-4+2i; %输入三个复数向量
subplot(1,2,1);compass([A1,A2,A3],'b') %绘制罗盘图
title('罗盘图');
subplot(1,2,2);feather([A1,A2,A3],'r') %绘制羽毛图
title('羽毛图');figure
quiver([0,1,2],0,[real(A1),real(A2),real(A3)],..., %绘制向量场图
[imag(A1),imag(A2),imag(A3)],'b')
title('向量场图')
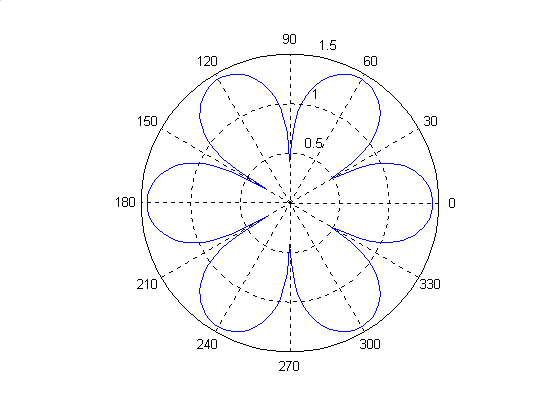
1.3.6. 极坐标图
MATLAB提供polar函数绘制极坐标图,函数调用格式如下:
polar(theta,rho,’参数’)
其中,theta为相角,以弧度为单位;rho为半径;参数定义与plot函数相同。
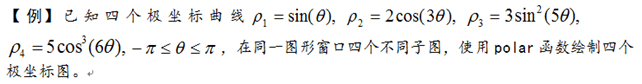
theta=-pi:0.01:pi;rho1=sin(theta);
rho2=2*cos(3*theta);
rho3=3*sin(5*theta).^2;
rho4=5*cos(6*theta).^3;
subplot(2,2,1);polar(theta,rho1)
title('sin()')
subplot(2,2,2);polar(theta,rho2,'r')
title('2*cos(3) ')
subplot(2,2,3);polar(theta,rho3,'g')
title('3*sin2(5) ')
subplot(2,2,4);polar(theta,rho4,'c')
title('5*cos3(6) ')
1.3.7. 对数坐标图
MATLAB提供semilogx和semilogy函数实现对x轴和y轴的半对数坐标图,提供loglog函数实现双对数坐标图。它们的调用格式如下:
(1)semilogx(x1,y1,’参数1’,…)% x轴为常用对数刻度,y轴为线性坐标刻度
(2)semilogy(x1,y1,’参数1’,…)% x轴为线性坐标刻度,y轴为常用对数刻度
(3)loglog(x1,y1,’参数1’,…) % x和y轴均采用常用对数刻度
其中,参数的定义和plot函数参数定义相同,所不同的是坐标轴的选取。
【例】在同一图形窗口,四个不同子图中绘制 函数的线性坐标,半对数坐标和双对数坐标图。
x=0:0.1:8;y=5*x.^3;
subplot(2,2,1);plot(x,y)
title('线性坐标图')
subplot(2,2,2);semilogx(x,y,'r-.')
title('半对数坐标图x')
subplot(2,2,3);semilogy(x,y,'g-')
title('半对数坐标图y')
subplot(2,2,4);loglog(x,y,'c--')
title('双对数坐标图')
1.3.8. 双纵坐标绘图
MATLAB提供plotyy函数实现把函数值具有不同量纲、不同数量级的两个函数绘制在同一坐标系中。
plotyy函数的调用格式为:
(1) plotyy(x1,y1,x2,y2)
(2) plotyy(x1,y1,x2,y2,fun1,fun2)
其中,横坐标的刻度相同,左纵坐标用于x1,y1数据绘图,右纵坐标用于x2,y2数据绘图;fun1和fun2是句柄或字符串,控制作图的方式,fun可以为plot, semilogx, semilogy, loglog, stem等二维绘图指令。
【例】在同一图形窗口,实现两条曲线y1=3sin(x) ,的双纵坐标绘图。
x=0:0.1:6;y1=3*sin(x);y2=2*x.^2;
subplot(1,2,1);plotyy(x,y1,x,y2)
title('绘制线性双纵坐标图')
grid on
subplot(1,2,2);
plotyy(x,y1,x,y2,'plot','semilogy')
title('线性和半对数双纵坐标图')
grid on
1.3.9. 函数绘图
(1)ezplot(f)
其中,x是默认取值范围,绘制f=f(x)的图形。对于 f(x , y), x和y的默认取值范围都是,,绘制f(x,y)=0的图形。
(2)ezplot(f,[min,max])
其中,x是的取值范围是,绘制f=f(x)的图形。
(3)ezplot(x,y)
按照t的默认取值范围绘制函数x=x(t)、y=y(t)的图形。
(4)ezplot(x,y,[tmin,tmax])
按照t的取值范围(),绘制函数x=x(t)、y=y(t)的图形。
【例】在同一图形窗口,不同子窗口下,用ezplot函数绘制两条曲线 。
clear;
f1='sin(2*x)';f2='x.^2-y.^2-1';
subplot(1,2,1);
ezplot(f1,[0,2*pi])
title('f=sin(2*x)');grid on
subplot(1,2,2);
ezplot(f2)
title('x^2-y^2-1');grid on
1.4. 三维曲线和曲面的绘制
1.4.1. 绘制三维线图
三维曲线图是根据三维坐标(x,y,z)绘制的曲线,MATLAB使用plot3函数实现。其调用格式和二维绘图的plot命令相似,命令格式为:
plot3(x,y,z,’选项’) %绘制三维曲线
其中,x,y,z必须是同维的向量或者矩阵,若是向量时,则绘制一条三维曲线,若是矩阵时,按矩阵的列绘制多条三维曲线,三维曲线的条数等于矩阵的列数。选项的定义和二维plot函数定义一样。
【例】绘制三维曲线,当x为矩阵和向量,y=sin(x), z=cos(x)时。
x=[0:0.1:2*pi;4*pi:0.1:6*pi]';
y=sin(x);z=cos(x);
subplot(1,2,1);plot3(x,y,z)
title('矩阵的三维曲线绘制')
x1=[0:0.2:10*pi];
y1=cos(x1);z1=sin(x1);
subplot(1,2,2);plot3(x1,y1,z1,'r-.*')
title('向量的三维曲线绘制')
grid on
1.4.2. 绘制三维曲面图
1.三维网格图
MATLAB提供mesh函数绘制三维网格图,其调用格式如下:
mesh(X,Y,Z,C)
其中,X,Y是通过meshgrid得到的网格顶点;C是指定各点的用色矩阵。C可以默认省略。
meshgrid函数是用来在(x,y)平面上产生矩形网格,其调用格式为:
[X,Y]=meshgrid(x,y)
其中若x和y分别为n个和m个元素的一维数组,则X和Y都是的矩阵,每个(X,Y)对应一个网格点;如果y省略,则X和Y都是的方阵。
另外,mesh函数还派生出另外两个函数meshc和meshz,meshc用来绘制带有等高线的三维网格图;meshz是用来绘制带基准平面的三维网格图,用法和mesh类似。
【例】已知 ,,分别使用plot3,mesh,meshc和mechz,绘制三维曲线和三维网格图。
x=-5:0.2:5;[X,Y]=meshgrid(x);Z=X.^2-Y.^2;
subplot(2,2,1);plot3(X,Y,Z) %绘制三维曲线
title('plot3')
subplot(2,2,2);mesh(X,Y,Z) %绘制三维网格图
title('mesh')
subplot(2,2,3);meshc(X,Y,Z) %绘制带等高线的三维网格图
title('meshc')
subplot(2,2,4);meshz(X,Y,Z) %绘制带基准平面的三维网格图
title('meshz')
2.三维表面图
MATLAB提供surf函数,实现绘制三维表面图,也是需要生成网格等点(X,Y),再计算出Z,函数调用格式为:
surf(X,Y,Z,C) %绘制三维表面图
其中参数定义和mesh参数定义相同。
另外,surf函数还派生出另外两个函数surfc和surfl,surfc用来绘制带有等高线的三维表面图;surfl是用来绘制带光照效果的三维表面图,用法和surf类似。
2.三维表面图
【例】在上作出 所对应的三维表面图。
x=-5:0.3:5;
y=-3:0.2:3;
[X,Y]=meshgrid(x,y);
Z=sqrt(X.^4.*Y.^2);
subplot(2,2,1);mesh(X,Y,Z)
title('mesh')
subplot(2,2,2);surf(X,Y,Z)
title('surf')
subplot(2,2,3);surfc(X,Y,Z)
title('surfc')
subplot(2,2,4);surfl(X,Y,Z)
title('surfl')
1.4.3. 特殊的三维图形
MATLAB提供很多函数绘制特殊的三维图形,比如三维柱状图bar3,bar3h,饼图pie3,火柴杆图stem3,这些函数在二维特殊图形绘制章节顺带介绍过了,不再赘述。下面主要介绍一下三维等高线图和瀑布图。
1. 等高线图
等高线图常用于地形绘制中,MATLAB提供contour3函数用于绘制等高线图,它能自动根据z值的最大值和最小值来确定等高线的条数,也可以根据给定参数来取值。函数调用格式为:
contour3(X,Y,Z,n) %绘制等高线图
其中,X,Y和Z定义和mesh的X,Y和Z定义一样,n为给定等高线的条数,若n省略,则自动根据z值确定等高线的条数。
2. 瀑布图
瀑布图和网格图很相似,不同的是瀑布图把每条曲线都垂下来,形成瀑布状。MATLAB提供waterfall函数绘制瀑布图。函数调用格式为:
waterfall(X,Y,Z) %绘制瀑布图
其中X,Y和Z定义和mesh的X,Y和Z定义一样,X和Y还可以省略。
【例】在上,作出所对应的等高线图,瀑布图,和三维网格图。
x=-5:0.3:5;
y=-3:0.2:3;
[X,Y]=meshgrid(x,y);
Z =sin(sqrt(X.^2+Y.^2));
subplot(2,2,1);contour3(X,Y,Z)
title('默认值的等高线图')
subplot(2,2,2);contour3(X,Y,Z,30);
title('给定值的等高线图')
subplot(2,2,3);waterfall(X,Y,Z);
title('瀑布图')
subplot(2,2,4);mesh(X,Y,Z);
title('三维网格图')
1.4.4. 绘制动画图形
MATLAB可以利用函数(movie、getframe和moviein)实现动画的制作。原理是先把帧帧二维或者三维图形存储起来,然后利用命令把这些帧图形回放,达到产生动画效果。函数调用格式为:
(1)movie(M, k)%播放动画
其中,M是要播的画面矩阵,k如果是一个数,为播放次数。k如果是一个向量,则第一个元素为播放次数,后面向量组成播放帧的清单。
(2)M(i)=getframe %录制动画的每一帧图形
(3)M=moviein(n) %预留分配存储帧的空间
其中,n为存储放映帧数,M预留分配存储帧的空间。
【例】矩形函数的傅里叶变换时sinc函数,sinc(r)=sin(r)/r,其中r是X-Y平面上的向径。用surfc命令,制作sinc函数的立体图,并采用动画函数,播放动画效果。
x=-9:0.2:9;[X,Y]=meshgrid(x);
R=sqrt(X.^2+Y.^2)+eps;Z =sin(R)./R;
h=surfc(X,Y,Z); %产生每帧数据
M=moviein(20); %预先分配一个能存储20帧的矩阵
for i=1:20
rotate(h,[0 0 1],15); %使得图形绕z轴旋转15度/每次
M(i)=getframe; %录制动画的每一帧
end
movie(M,10,6) %每秒6帧速度,重复播放10次
1.5. MATLAB图形窗口
MATLAB图形窗口不仅仅是绘图函数和工具形成的显示窗口,而且还是利用图形窗口编辑图形。前面本章介绍的很多图形制作和图形修饰命令,都可以利用MATLAB图形窗口操作实现。
MATLAB的图形窗口界面如下图所示,分为4个部分:图形窗口标题栏、菜单栏、快捷工具栏和图形显示窗口。图形窗口的菜单栏是编辑图形的主要部分,很多菜单按键和Windows标准按键相同,不再赘述。

利用图形窗口对曲线和图形编辑和修饰用的比较多的是“插入”菜单。插入菜单主要用于向当前图形窗口中插入各种标注图形,包括:X轴标签,Y轴标签,Z轴标签,图形标题,图例,颜色栏,直线,箭头,文本箭头,双向箭头,文本,矩形,椭圆,坐标轴和灯光。
图形窗口的快捷工具栏有:编辑绘图键,放大键,缩小键,平移键,三维旋转,数据游标,刷亮/选择数据,链接绘图,插入颜色栏,插入图例,隐藏绘图工具键,显示绘图工具键。