1. Matlab数值计算
1.1. 多项式运算
多项式在代数中占有重要的地位,广泛用于数据插值、数据拟合和信号与系统等应用领域。
1.1.1. 多项式的创建
一个多项式按降幂排列为:
在MATLAB中多项式的各项系数用一个行向量表示,使用长度为n+1 的行向量按降幂排列,多项式中某次幂的缺项用0表示,则表示为:
例如,可表示为
可以用poly2str,poly2sym函数创建一个多项式,其格式如下:
f = poly2str(p,'x') % p为多项式的系数,x多项式的变量
f =poly2sym(p) % p 为多项式的系数
其中,f =poly2str(p,'x')表示创建一个系数为p,变量为x的字符串型多项式;f = poly2sym(p)表示创建一个符号型多项式。两者在命令窗口显示形式类似,但数据类型不一样,一个是字符串型,另一个是符号型。
【例】已知多项式系数为 p=[1 -2 4 6],分别用poly2str(p,'x')和poly2sym(p)创建多项式,比较它们有什么不同。
程序代码如下:
>> p=[1 -2 4 6]
p = 1 -2 4 6
>> f1=poly2str(p,'x')
f1 = x^3 - 2 x^2 + 4 x + 6
>> f2=poly2sym(p)
f2 =x^3 - 2*x^2 + 4*x + 6
显然,两种函数创建的多项式f1和f2显示形式类似,但数据类型和大小都不一样,如下图所示。
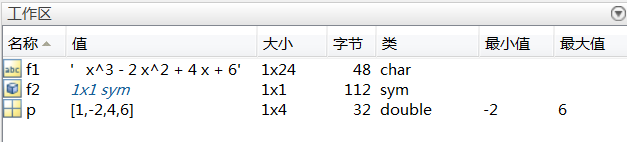
1.1.2. 多项式的值和根
1.多项式的值
(1)矩阵多项式求值
polyvalm函数以矩阵为自变量求多项式的值,其调用格式为:Y=polyvalm(p,X)
其中p为多项式系数,X为自变量,要求为方阵。
polyvalm和polyval函数求多项式的值是不一样,因为运算规则不一样。例如,假设A为方阵,p为多项式 的系数,则:
polyvalm(p,A)表示:
而polyval(p,A)表示:
求多项式的值可以用polyval和polyvalm函数。
(2)代数多项式求值
polyval函数可以求代数多项式的值,其调用格式为:
y=polyval(p,x)
其中当x为一个数值,则求多项式在该点的值;若x为向量或矩阵,则对向量或矩阵每个元素求多项式的值。
【例4-2】已知多项式为 ,分别求x1=2和x=[0,2,4,6,8,10]向量的多项式的值。
x1=2;
x=[0:2:10];
p=[1 -2 4 6];
y1=polyval(p,x1)
y=polyval(p,x)
程序运行结果:
>>
y1 = 14
y = 6 14 54 174 422 846
【例】已知多项式为 ,分别用polyvalm和polyval函数,求的多项式值。
程序代码如下:
X=[1 2;3 4];
p=[1 -3 2];
Y=polyvalm(p,X)
Y1=polyval(p,X)
程序运行结果:
>>
Y = 6 4
6 12
Y1 = 0 0
2 6
2.多项式的根
roots函数用于求多项式的全部根,其调用格式为:
r=roots(p)
其中,p为多项式的系数向量,r为多项式的根向量。
已知多项式的根,可以用poly函数求多项式的系数。其格式为:
p=poly(r)
其中,r为多项式的根,p为由根r构造的多项式系数向量。
【例】已知多项式为。
(1)用roots函数求该多项式的根r;
(2)用poly函数求根为r的多项式系数。
程序代码如下:
p=[1 4 0 -3 2];
r=roots(p)
p1=poly(r)
程序运行结果:
>>
r =
-3.7485 + 0.0000i
-1.2962 + 0.0000i
0.5224 + 0.3725i
0.5224 - 0.3725i
p1 = 1.0000 4.0000 -0.0000 -3.0000 2.0000
显然,roots和poly函数的功能正好相反。
1.1.3. 多项式的四则运算
多项式系数向量进行四则运算,得到的结果仍为多项式系数向量。
1.多项式的加减运算
多项式的加减运算,是合并同类项,可以用系数向量相加减运算。如果多项式阶次不同,则把低次多项式系数不足的高次项用0补足。
2.多项式乘法运算
两个多项式的乘积可以用函数conv实现。其调用格式为:
p=conv(p1,p2)
其中p1和p2是多项式的系数向量;p是两个多项式乘积的系数向量
3.多项式除法运算
函数deconv实现两个多项式的除法运算。其调用格式为:
[q,r]=deconv(p1,p2)
其中,q为多项式p1除以p2的商式;r为多项式p1除以p2的余式。q和r都是多项式系数向量。
deconv是conv的逆函数,即有p1=conv(p2,q)+r
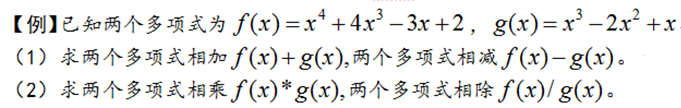
程序代码如下:
p1=[1 4 0 -3 2];
p2=[0 1 -2 1 0];
p3=[1 -2 1 0];
p=p1+p2
poly2sym(p)
p=p1-p2
poly2sym(p)
p=conv(p1,p2)
poly2sym(p)
[q,r]=deconv(p1,p3)
p4=conv(q,p3)+r
程序运行结果:
>>
p = 1 5 -2 -2 2
ans =x^4 + 5*x^3 - 2*x^2 - 2*x + 2
p = 1 3 2 -4 2
ans = x^4 + 3*x^3 + 2*x^2 - 4*x + 2
p = 0 1 2 -7 1 8 -7 2 0
ans = x^7 + 2*x^6 - 7*x^5 + x^4 + 8*x^3 - 7*x^2 + 2*x
q = 1 6
r = 0 0 11 -9 2
p4 = 1 4 0 -3 2
1.1.4. 多项式的微积分运算
1.多项式的微分
polyder函数可以求多项式的微分运算,polyder函数可以对单个多项式求导,也可以对两个多项式乘积和商求导,其调用格式如下:
p=polyder(p1) %求多项式p1的导数
p=polyder(p1,p2) %求多项式p1*p2的积的导数
[p,q]=polyder(p1,p2) %p1/p2的导数,p为导数的分子多项式系数,
%q为导数的分母多项式系数
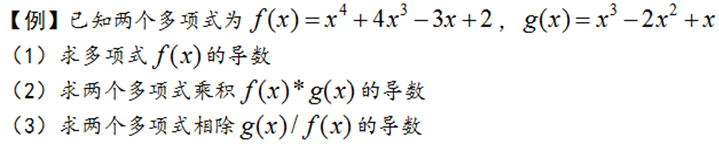
p1=[1 4 0 -3 2];
p2=[1 -2 1 0];
p=polyder(p1)
poly2sym(p)
p=polyder(p1,p2)
poly2sym(p)
[p,q]=polyder(p2,p1)
>>
p = 4 12 0 -3
ans = 4*x^3 + 12*x^2 - 3
p = 7 12 -35 4 24 -14 2
ans = 7*x^6 + 12*x^5 - 35*x^4 + 4*x^3 + 24*x^2 - 14*x + 2
p = -1 4 5 -14 12 -8 2
q = 1 8 16 -6 -20 16 9 -12 4
2.多项式的积分
polyint函数用于多项式的积分。其调用格式为:
- I=polyint(p,k) %求以p为系数的多项式的积分,k为积分常数项
- I=polyint(p) %求以p为系数的多项式的积分,k默认值0
显然polyint是polyer的逆函数,即有p=polyder(I)
【例】求多项式的积分
程序代码如下:
p=[1 4 0 -3 2];
I=polyint(p)
poly2sym(I)
p=polyder(I)
syms k
I1=polyint(p,k)
poly2sym(I1)
程序运行结果:
>>
I = 0.2000 1.0000 0 -1.5000 2.0000 0
ans = x^5/5 + x^4 - (3*x^2)/2 + 2*x
p = 1 4 0 -3 2
I1 = [ 1/5, 1, 0, -3/2, 2, k]
ans =
x^5/5 + x^4 - (3*x^2)/2 + 2*x + k
1.1.5. 多项式的部分分式展开
由分子多项式B(s)和分母多项式A(s)构成的分式表达式进行多项式的部分分式展开,表达式如下:
MATLAB可以用residue函数实现多项式的部分分式展开,residue函数的调用格式如下:
[r,p,k]=residue(B,A)
其中,B为分子多项式系数行向量;A为分母多项式系数行向量;[ ]为极点列向量;[ ]为零点列向量;k为余式多项式行向量。
residue函数还可以将部分分式展示式转换为两个多项式的除的分式,其调用格式为
[B,A]=residue(r,p,k)
【例】已知分式表达式为 。
(1)求 的部分分式展开式。
(2)将部分分式展开式转换为分式表达式。
程序代码如下:
a=[1 -5 6];
b=[3 0 0 1]
[r,p,k]=residue(b,a)
[b1,a1]=residue(r,p,k)
程序运行结果:
>>
r = 82.0000
-25.0000
p = 3.0000
2.0000
k = 3 15
b1 = 3 0 0 1
a1 = 1 -5 6
1.2. 数值插值
MATLAB提供一维插值interp1、二维插值interp2、三维插值interp3和N维插值interpn函数,以及3次样条插值spline函数等。
1.2.1. 一维插值
指被插值函数的自变量是一个单变量的函数。一维插值采用的方法一般有一维多项式插值、一维快速插值和三次样条插值。
1.一维多项式插值
MATLAB中提供interp1函数进行一维多项式插值,格式如下:
yi=interp1(x,y,xi,method)
其中,x和y为既有数据的向量,其长度必须相同。xi为要插值的数据点向量。
- method插值方法,‘nearest’/‘linear’/’next’/’ previous’ ‘cubic’/‘spline’之一,分别为最近点插值/线性插值/下一点插值/前一点插值/三次多项式插值/三次样条插值。
MATLAB还提供interp1q函数也是用于一维插值。它与interp1函数的主要区别是,当已知数据不是等间距分布时,interp1q插值速度比interp1快。interp1q执行的插值数据x必须是单调递增的。
【例】某气象台对当地气温进行测量,实测数据见下表所示,用不同插值方法计算t=12点处的气温。
| 测量时间t(小时) | 6 | 8 | 10 | 14 | 16 | 18 | 20 |
|---|---|---|---|---|---|---|---|
| 温度T(度) | 16 | 17.5 | 19.3 | 22 | 21.2 | 19.5 | 18 |
t=[6 8 10 14 16 18 20];
T=[16 17.5 19.3 22 21.2 19.5 18];
t1=12;
T1=interp1(t,T,t1,'nearest')
T2=interp1(t,T,t1,'linear')
T3=interp1(t,T,t1,'next')
T4=interp1(t,T,t1,'previous')
T5=interp1(t,T,t1,'cubic')
T6=interp1(t,T,t1,'spline')
程序运行结果:
>>
T1 = 22
T2 = 20.6500
T3 = 22
T4 = 19.3000
T5 = 21.0419
T6 = 21.1193
【例】假设测量的数据来自函数,试根据生成的数据,用不同方法进行插值,比较插值结果。
程序代码如下:
clear
x=(0:0.4:2*pi)';
y=exp(-0.5*x).*sin(x);
x1=(0:0.1:2*pi)';
y0=exp(-0.5*x1).*sin(x1);
y1=interp1(x,y,x1,'nearest');
disp('interp1函数插值时间');tic
y2=interp1(x,y,x1); toc;
y3=interp1(x,y,x1,'spline') ;
disp('interp1q函数插值时间');tic
yq=interp1q(x,y,x1);toc;
plot(x1,y1,'--',x1,y2,'-',x1,y3,'-.',x,y,'*',x1,y0,':')
legend('nearest插值数据','linear插值数据','spline插值数据',...
'样本数据点','插值点真实数据')
max(abs(y0-y3))
程序运行结果如下,插值效果如下图所示。
>>
interp1函数插值所需时间:
时间已过 0.001926 秒。
interp1q函数插值所需时间:
时间已过 0.000790 秒。
ans = 7.0467e-04
二、一维快速傅里叶插值
一维快速傅里叶插值可以用interpft函数实现。该函数利用傅里叶变换将输入数据变换到频率域,实现对数据的插值。
函数调用格式为:
y=interpft(x,n) %表示对x进行傅里叶变换,然后采用n点傅里叶逆变换,得到插值后的数据。
y=interpft(x,n,dim) %表示在dim维上进行傅里叶插值。
【例】假设测量的数据来自函数 ,试根据生成的数据,用一维快速傅里叶插值,比较插值结果。
程序代码如下
clear
x=0:0.4:2*pi;
y=sin(x);
N=length(y);
M=N*4;
x1=0:0.1:2*pi;
y1=interpft(y,M-1);
y2=sin(x1);
plot(x,y,'O',x1,y1,'*',x1,y2,'-')
legend('原始数据','¸傅里叶插值数据','插值点真实数据')
max(abs(y1-y2))
程序运行结果如下,插值效果如下图所示。
>>
ans = 0.0980
3.三次样条插值
三次样条插值是利用多段多项式逼近插值,降低插值多项式的阶数,使得曲线更为光滑。在MATLAB中,interp1插值函数的method选为spline样条插值选项,就可以实现三次样条插值。
另外,MATLAB专门提供三次样条插值函数spline,
其格式如下:
yi=spline(x,y,xi) %利用初始值x,y,对插值点数据xi进行三次样条插值。采用这种调用方式,相当于yi=interp1(x,y,xi,’spline’).
【例】已知数据x=[-5 -4 -3 -2 -1 0 1 2 3 4 5],y=[25 16 9 4 1 0 1 4 9 16 25],对xi=-5:0.5:5,用spline进行三次样条插值,并比较用interp1实现三次样条插值。
x=-5:5;y=x.*x;
xi=-5:0.5:5;y0=xi.*xi;
y1=spline(x,y,xi);
y2=interp1(x,y,xi,'spline');
plot(x,y,'O',xi,y0,xi,y1,'+',xi,y2,'*')
legend('原始数据','插值点真实数据','spline插值','interp1样条插值')
max(abs(y1-y2))
1.2.2. 二维插值
interp2函数用于实现二维插值,其调用格式为:
Z1=interp2(X,Y,Z,X1,Y1,’method’)
其中,X,Y是两个参数的采样点,一般是向量,Z是参数采样点对应的函数值。X1,Y1是插值点,可以是标量也可以是向量。Z1是根据选定的插值方法(method)得到的插值结果。插值方法method和一维插值函数相同。需要注意,X1和Y1不能超出X,Y的取值范围,否则会得到NaN错误信息。
【例】某实验对电脑主板的温度分布做测试。用x表示主板的宽度(cm),y表示主板的深度(cm),用T表示测得的各点温度(ºC),测量结果如下表所示。
(1)分别用最近点二维插值和线性二维插值法求(12.6,7.2)点的温度;
(2)用三次多项式插值求主板宽度每1cm,深度每1cm处各点的温度,并用图形显示插值前后主板的温度分布图。
| y x | 0 | 5 | 10 | 15 | 20 | 25 |
|---|---|---|---|---|---|---|
| 0 | 30 | 32 | 34 | 33 | 32 | 31 |
| 5 | 33 | 37 | 41 | 38 | 35 | 33 |
| 10 | 35 | 38 | 44 | 43 | 37 | 34 |
| 15 | 32 | 34 | 36 | 35 | 33 | 32 |
clear
x=[0:5:25];
y=[0:5:15]';
T=[30 32 34 33 32 31;
33 37 41 38 35 33;
35 38 44 43 37 34;
32 34 36 35 33 32];
x1=12.6;y1=7.2;
T1=interp2(x,y,T,x1,y1,'nearest')
T2=interp2(x,y,T,x1,y1,'linear')
xi=[0:1:25];yi=[0:1:15]';
Ti=interp2(x,y,T,xi,yi,'cubic');
subplot(1,2,1)
mesh(x,y,T)
xlabel('板宽度(cm)');ylabel('板深度(cm)');zlabel('温度(摄氏度)')
title('插值前主板温度分布图')
subplot(1,2,2)
mesh(xi,yi,Ti)
xlabel('板宽度(cm)');ylabel('板深度(cm)');zlabel('温度(摄氏度)')
title('插值后主板温度分布图')
运行程序,结果如下
>>
T1 = 38
T2 = 40.0400
1.2.3. 多维插值
1. 三维插值
在MATLAB中,还提供了三维插值的函数interp3,其调用格式为:
U1=interp3(X,Y,Z,U,X1,Y1,Z1,’method’)
其中,X, Y, Z是三个参数的采样点,一般是向量,U是参数采样点对应的函数值。X1,Y1, Z1是插值点,可以是标量也可以是向量。U1是根据选定的插值方法(method)得到的插值结果。插值方法method和一维插值函数相同。需要注意,X1,Y1和Z1不能超出X,Y,Z的取值范围,否则会得到NaN错误信息。
2. n维插值
在MATLAB中,interpn函数用于实现n维插值。其调用格式为:
其中,是n个参数的采用点,一般是向量,U是参数采样点对应的函数值。U是插值点,可以是标量也可以是向量。U1是根据选定的插值方法(method)得到的插值结果。插值方法method和一维插值函数相同。需要注意, 不能超出的取值范围,否则会得到NaN错误信息。
3. 数据拟合
与数据插值类似,数据拟合的目的也是用一个较为简单的函数g(x)去逼近一个未知的函数f(x)。利用已知测量的数据(xi,yi)(i=1,2,..,n),构造函数y=g(x),使得误差:
在某种意义上达到最小。
在MATLAB中,用polyfit函数可以实现最小二乘意义的多项式拟合。polyfit拟合函数求的是多项式的系数向量。
该函数的调用格式为:
p=polyfit(x,y,n)
[p,S]=polyfit(x,y,n)
其中,p为最小二乘意义上的n阶多项式系数向量,长度为n+1,x,y为数据点向量,要求是等长的向量,S为采样点的误差结构体,包括R,df和normr分量,分别表示对x进行QR分解三角元素,自由度和残差。
【例】在MATLAB中,用polyfit函数实现一个4阶和5阶多项式在区间[0,3*pi]内逼近函数,利用绘图的方法,比较拟合的4阶多项式、5阶多项式和的区别。
程序代码如下:
clear
x=linspace(0,3*pi,30);
y=exp(-0.5*x).*sin(x);
[p1,s1]=polyfit(x,y,4)
g1=poly2str(p1,'x')
[p2,s2]=polyfit(x,y,5)
g2=poly2str(p2,'x')
y1=polyval(p1,x);
y2=polyval(p2,x);
plot(x,y,'-*',x,y1,':O',x,y2,':+')
legend('f(x)','4阶多项式','5阶多项式')
>>
p1 = -0.0024 0.0462 -0.2782 0.4760 0.1505
g1 = -0.002378 x^4 + 0.04625 x^3 - 0.27815 x^2 + 0.476 x + 0.15048
p2 =0.0007 -0.0191 0.1856 -0.7593 1.0826 0.0046
g2 = 0.00071166 x^5 - 0.019146 x^4 + 0.18564 x^3 - 0.75929 x^2 + 1.0826 x + 0.0045771
1.3. 数据统计
1.3.1. 矩阵元素的最大值和最小值
1.求向量的最大元素和最小元素
(1)求向量的最大元素
求一个向量X的最大元素可以用函数max(X),其调用格式为:
y=max(X) %返回向量X的最大元素给y,如果X中包括复数
%元素,则按模取最大元素。
[y,k]=max(X)%返回向量X的最大元素给y,最大元素所在的位置序号给k。
(2)求向量的最小元素
求一个向量X的最小元素可以用函数min(X),其调用格式及用法与max(X) 函数一样。
例求向量X=[34,23,-23,6,76,56,14,35]的最大值。
>> X=[34,23,-23,6,76,56,14,35];
>> y=max(X)
y = 76
>> [y,k]=max(X)
y = 76
k = 5
>> y=min(X)
y = -23
>> [y,k]=min(X)
y = -23
k = 3
>> [Y2,K]=min(A,[],2) %求每行最小元素,及每行最小值的列数
Y2 = -6
-4
-3
-7
K = 3
1
2
4
>> Y3=max(A) %求每列的最大元素
Y3 = 45 23 18 24
>> [Y4,K1]=min(A) %求每列的最小元素,及最小元素所在的行数
Y4 = -4 -3 -6 -7
K1 = 2 3 1 4
>>ymax=max(max(A)) %求矩阵A的最大元素
ymax =
45
>>ymin=min(min(A)) % 求矩阵A的最小元素
ymin =
-7
3. 两个维度一样的向量或矩阵对应元素比较
例求A和B矩阵对应元素的较大元素Y1和较小元素Y2。
程序代码如下:
>> A=[1 5 6;7 3 1;3 7 4]
A =
1 5 6
7 3 1
3 7 4
>> B=[2 9 4;9 1 3;-1 0 3]
B =
2 9 4
9 1 3
-1 0 3
max和min函数还能对两个维度一样的向量或矩阵对应元素求大值和小值。
Y=max(A, B)
其中A和B是同维度的向量或矩阵,Y的每个元素为A和B对应元素的较大者,与A和B同维。
min函数的用法和max一样。
1.3.2. 矩阵元素的平均值和中值
求矩阵或向量元素的平均值用mean函数,求中值用median函数。
(1)y=mean(X) %返回向量X的算术平均值。
(2)Y=mean(A) %返回一个矩阵A每列的算术平均值的行向量。
(3)y=median(X) %返回向量X的中值。
(4)Y=median(A) %返回一个矩阵A每列的中值的行向量。
(5)Y=mean(A,dim) %当dim为1时,等同于mean(A);当dim
%为2时,返回一个矩阵A每行的算术平均值的列向量。
(6)Y=median(A,dim)%dim为2时,返回每行的中值的列向量。
例如,求向量X和矩阵A的平均值和中值。
>> X=[1,12,23,7,9,-5,30];
>> y1=mean(X)
y1 = 11
>> y2=median(X)
y2 = 9
>> A=[0 9 2;7 3 3;-1 0 3];
>> Y1=mean(A)
Y1 = 2.0000 4.0000 2.6667
>> Y2=median(A)
Y2 = 0 3 3
>> Y3=mean(A,2)
Y3 = 3.6667
4.3333
0.6667
>> Y4=median(A,2)
Y4 = 2
3
0
1.3.3. 矩阵元素的排序
对于向量X的排序,可以用函数sort(X),返回按升序排列的向量。
[Y,I]=sort(A, dim, mode) %对矩阵A的各行或各列的元素重新排序
其中,当dim为1时,按列排序;当dim为2时,按行排序。
dim默认为1。当mode为‘ascend’,则按升序排序;当mode为‘descend’,则按降序排序。mode默认取‘ascend’。Y为排序后的矩阵,而I记录Y中元素在A中的位置。
例如,对一个向量X和一个矩阵A做各种排序。
>> X=[1,12,23,7,9,-5,30];
>> Y=sort(X)
Y = -5 1 7 9 12 23 30
>> A=[0 9 2;7 3 1;-1 0 3];
>> Y1=sort(A)
Y1 = -1 0 1
0 3 2
7 9 3
>> Y2=sort(A,1,'descend')
Y2 = 7 9 3
0 3 2
-1 0 1
>> Y3=sort(A,2,'ascend')
Y3 = 0 2 9
1 3 7
-1 0 3
>> [Y4,I]=sort(A,2,'descend')
Y4 = 9 2 0
7 3 1
3 0 -1
I = 2 3 1
1 2 3
3 2 1
1.3.4. 矩阵元素求和和求积
在MATLAB中,向量和矩阵求和与求积的基本函数是sum和prod,调用格式为:
(1)y=sum(X) %返回向量X各元素的和。
(2)y=prod(X) %返回向量X各元素的乘积。
(3)Y=sum(A) %返回一个矩阵A各列元素的和的行向量。
(4)Y=prod(A) %返回一个矩阵A各列元素的乘积的行向量。
(5)Y=sum(A,dim) %当dim为1时,该函数等同于sum(A);当dim为2时,返回一个矩阵A各行元素的和的列向量。
例如,求一个向量X和一个矩阵A的各元素的和与乘积
>> X=[1,3,9,-2,7];
>> y=sum(X)
y = 18
>> y=prod(X)
y = -378
>> A=[1 9 2;7 3 1;-1 1 3]
A = 1 9 2
7 3 1
-1 1 3
>> Y1=sum(A)
Y1 = 7 13 6
>> Y2=sum(A,2)
Y2 = 12
11
3
>> Y3=prod(A)
Y3 = -7 27 6
>> Y4=prod(A,2)
Y4 = 18
21
-3
>> y5=sum(Y1)
y5 = 26
>> y6=prod(Y3)
y6 = -1134
1.3.5. 矩阵元素的累加和与累乘积
向量和矩阵的累加和与累乘积的基本函数是cumsum和cumprod。
(1)y=cumsum(X) %返回向量X累加和向量。
(2)y=cumprod(X) %返回向量X累乘积向量。
(3)Y=cumsum(A) %返回一个矩阵A各列元素的累加和的矩阵。
(4)Y=cumprod(A) %返回一个矩阵A各列元素的累乘积的矩阵。
(5)Y=cumsum(A,dim) %当dim为1时,该函数等同于cumsum(A);
当dim为2时,返回一个矩阵A各行元素的累加和矩阵。
(6)Y=cumprod(A,dim) %当dim为2时,返回各行元素的累乘积矩阵。
例如,求一个向量X和一个矩阵A的各元素的累加和与累乘积
>> X=[1,3,9,-2,7];
>> Y=cumsum(X)
Y = 1 4 13 11 18
>> Y=cumprod(X)
Y = 1 3 27 -54 -378
>> A=[1 9 2;7 3 1;-1 1 3]
A = 1 9 2
7 3 1
-1 1 3
>> Y1=cumsum(A)
Y1 = 1 9 2
8 12 3
7 13 6
>> Y2=cumsum(A,2)
Y2 = 1 10 12
7 10 11
-1 0 3
>> Y3=cumprod(A)
Y3 = 1 9 2
7 27 2
-7 27 6
>> Y4=cumprod(A,2)
Y4 = 1 9 18
7 21 21
-1 -1 -3
1.3.6. 标准方差和相关系数
- 标准方差
对于向量X,std(X)返回一个标准方差;对于矩阵A,std(A)返回一个矩阵A各列或者各行的标准方差向量。std函数的调用格式为:
(1)d=std(X) %求向量X的标准方差。
(2)D=std(A,flag,dim)
其中,当dim为1时,求矩阵A的各列元素的标准方差;当dim为2时,则求矩阵A的各行元素的标准方差。当flag为0时,按公式D1计算标准方差;当flag为1时,按D2计算标准方差。默认flag=0,dim=1。
例如,求一个向量X和一个矩阵A的标准方差。
>> X=[1,3,9,-2,7];
>> d=std(X)
d = 4.4497
>> A=[1 9 2;7 3 1;-1 1 3]
A = 1 9 2
7 3 1
-1 1 3
>> D1=std(A,0,1)
D1 = 4.1633 4.1633 1.0000
>> D2=std(A,0,2)
D2 = 4.3589
3.0551
2.0000
>> D3=std(A,1,1)
D3 = 3.3993 3.3993 0.8165
>> D4=std(A,1,2)
D4 = 3.5590
2.4944
1.6330
2. 相关系数
在MATLAB中,可以用函数corrcoef计算数据的相关系数。
(1)R=corrcoef(X,Y) %返回相关系数,其中X和Y是长度相等的向量。
(2)R=corrcoef(A) %返回矩阵A的每列之间计算相关形成的相关系数矩阵。
例如,求两个向量X和Y的相关系数,并求正态分布随机矩阵A的均值,标准方差和相关系数。
程序代码如下:
>> X=[1,3,9,-2,7];
>> Y=[2,3,7,0,6];
>> r=corrcoef(X,Y)
r = 1.0000 0.9985
0.9985 1.0000
>> A=randn(1000,3);
>> y=mean(A)
y = 0.0253 0.0042 0.0427
>> D=std(A)
D = 0.9902 0.9919 1.0014
>> R=corrcoef(A)
R =
1.0000 0.0023 -0.0028
0.0023 1.0000 0.0454
-0.0028 0.0454 1.0000
由上述结果可知,每列的均值接近0,每列的标准方差接近1,验证了A为标准正态分布随机矩阵。
1.4. 数值计算
1.4.1. 函数极值
MATLAB求函数的极小值使用fminbnd和fminsearch函数。
1.一元函数的极值
fminbnd函数可以获得一元函数在给定区间内的最小值,函数调用格式如下:
(1)x=fminbnd(fun,x1,x2)
其中,fun是函数的句柄或匿名函数;x1和x2是寻找函数最小值的区间范围x1\<x\<x2;x为在给定区间内,极值所在的横坐标。
(2)[x,y]= fminbnd(fun,x1,x2) %y为求得的函数极值点处的函数值
【例】已知 ,在区间内,使用fminbnd函数获取y函数的极小值。
clear
x1=0;x2=5*pi;
fun=@(x)(exp(-0.2*x)*sin(x));
[x,y1]=fminbnd(fun,x1,x2)
x=0:0.1:5*pi;
y=exp(-0.2*x).*sin(x);
plot(x,y)
grid on
程序运行结果
>>
x =
4.5150
y1 =
-0.3975
2.多元函数的极值
fminsearch函数可以获得多元函数的最小值,使用该函数时须要指定开始的初始值,获得初始值附近的局部最小值。该函数调用格式如下:
(1)x = fminsearch(fun, x0)
(2)[x,y]= fminsearch(fun, x0)
其中,fun是多元函数的句柄或匿名函数;x0是给定的初始值;x是最小值的取值点;y是返回的最小值,可以省略。
【例】使用fminsearch函数获取 二元函数在初始值(0, 0)附近的极小值,已知 。
程序代码如下:
clear
fun=@(x)(100*(x(2)-x(1)^2)^2+(1-x(1))^2); %创建句柄函数
x0=[0,0];
[x,y1]=fminsearch(fun,x0) %计算局部函数的极小值
程序运行结果如下:
>>
x = 1.0000 1.0000
y1 = 3.6862e-10
由结果可知,由函数fminsearch计算出局部最小值点是[1, 1],最小值为y1 = 3.6862e-10,和理论上是一致的。
1.4.2. 函数零点
MATLAB可以使用fzero函数求零点,该函数的调用格式为:
(1)x=fzero(fun, x0)
(2)[x,y]=fzero(fun, x0)
其中,x为过零点的位置,如果找不到,则返回NaN;y是指函数在零点处函数的值;fun是函数句柄或匿名函数;x0是一个初始值或初始值区间。
只能返回一个局部零点,不能找出所有的零点,因此需要设定零点的范围。
【例】使用fzero函数求分别在初始值x0=0,x0=5附近的过零点,并求出过零点函数的值。
程序代码如下:
clear
fun=@(x)(x^2-5*x+4);
x0=0;
[x,y1]=fzero(fun,x0)
x0=5;
[x,y1]=fzero(fun,x0)
x0=[0,3];
[x,y1]=fzero(fun,x0)
程序运行结果如下:
>>
x = 1
y1 = 0
x = 4.0000
y1 = -3.5527e-15
x = 1
y1 = 0
1.4.3. 数值差分
在MATLAB中,没有直接求数值导数的函数,只有计算前向差分的函数diff,其调用格式为:
(1)D=diff(X) %计算向量X的向前差分,即
(2)D=diff(X, n) %计算向量X的n阶向前差分。即 diff(X, n)
=diff(diff(X,n-1))
(3)D=diff(A, n, dim) %计算矩阵A的n阶差分。当dim=1(默认),按行计算矩阵A的差分;当dim=2,按列计算矩阵的差分。
例如,已知矩阵 ,分别求矩阵A行和列的一阶和二阶前向差分。
>> A=[1 6 3;6 2 4;5 8 1]
A = 1 6 3
6 2 4
5 8 1
>> D=diff(A,1,1)
D = 5 -4 1
-1 6 -3
>> D=diff(A,1,2)
D =5 -3
-4 2
3 -7
>> D=diff(A,2,1)
D = -6 10 -4
>> D=diff(A,2,2)
D = -8
6
-10
1.4.4. 数值积分
1.一重数值积分
MATLAB提供了quad函数和quadl函数求一重定积分。它们调用格式为:
(1)q=quad(fun, a, b, tol, trace)
它是一种采用自适应的Simpson方法的一重数值积分,其中fun为被积函数,函数句柄;a和b为定积分的下限和上限;tol为绝对误差容限值,默认是10-6;trace控制是否展现积分过程,当trace取非0,则展现积分过程,默认取0。
(2)q=quadl(fun, a, b, tol, trace)
它是一种采用自适应的Lobatto方法的一重数值积分。参数定义和quad一样。
1.一重数值积分
【例】分别使用quad函数和quadl函数求的数值积分。
程序代码如下:
clear
fun=@(x)(exp(-0.2*x).*sin(x));
a=0;b=3*pi;
q1=quad(fun,a,b)
q2=quadl(fun,a,b)
q3=quad(fun,a,b,1e-3,1)
程序运行结果如下:
其中迭代过程最后一列的和为数值积分q3的值。
q1 =1.1075
q2 =1.1075
9 0.0000000000 2.55958120e+00 1.3793949196
11 0.0000000000 1.27979060e+00 0.6053358622
13 1.2797905993 1.27979060e+00 0.7742537042
15 2.5595811986 4.30561556e+00 -0.6459997048
17 2.5595811986 2.15280778e+00 -0.3430614927
19 4.7123889804 2.15280778e+00 -0.3052258622
21 6.8651967622 2.55958120e+00 0.3762543321
q3 = 1.1076
2.多重数值积分
MATLAB提供了dblquad函数和triplequad函数求二重积分和三重积分。它们调用格式为:
(1)q2=dblquad(fun, xmin, xmax, ymin,ymax, tol)
(2)q3=triplequad(fun, xmin, xmax, ymin, ymax, zmin, zmax, tol)
函数的参数定义和一重积分一样。
例如,求二重数值积分 。
代码如下:
>> q=dblquad('sin(x)*y+x*sin(y)',0,2*pi,0,3*pi)
q =
39.4784
1.4.5. 常微分方程求解
MATLAB为解常微分方程用的最多的是4/5阶龙格-库塔法ode45函数。
[t,y]=ode45(fun,ts,y0,options)
其中,fun是待解微分方程的函数句柄;ts是自变量范围,可以是范围[t0, tf],也可以是向量[t0,…,tf];y0是初始值,y0和y具有相同长度的列向量;options是设定微分方程解法器的参数,可以省略,也可以由odeset函数获得。
![C:\\Users\\xgb\\AppData\\Roaming\\Tencent\\Users\\779015031\\QQ\\WinTemp\\RichOle\\]4B4\$((}\$SY964V@}E7H]JU.png](media/f343c5805538ad45fd9dee89cdb5a697.png)
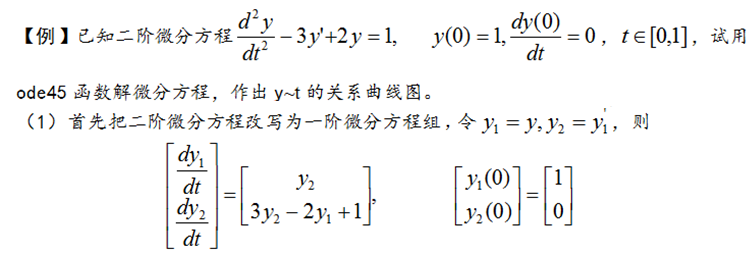
clear
t0=[0,1];
y0=[1;0];
[t,y]=ode45(@f04_20,t0,y0);
plot(t,y(:,1))
xlabel('t'),ylabel('y')
title('y(t)-t')
grid on
function y= f04_20(t,y)
%F04_20定义微分方程的函数文件
y=[y(2);3*y(2)-2*y(1)+1];
end
1.5. 建模案例
1.5.1. SIRS 模型
有些传染病(如流感、新冠肺炎等)愈后免疫力具有时效性,即康复者获得的免疫力不能终身保持,过一段时间后,康复者会丧失免疫力,再次成为易感者。
模型假设
- 假设总人数 N 保持不变,人群分为易感者、患病者和病愈免疫的康复者。时刻 t 三类人在总人数中所占比例分别记为 S(t)、I(t) 和 R(t),则 S(t)+I(t)+R(t) = 1 。
- 假设患病者的日接触率为 λ,日治愈率为 μ 。
- 假设每天丧失免疫力的康复者占康复者总数的比率为 γ(称为日丧失免疫率)
模型建立
从 t 到 t+Δt 三类人人数的增量分别为
记 t=0 时三类人的比例分别为 S0、I0 和 R0,则建立如下模型
此模型无解析解
1.5.2. SEIR 模型
有些传染病具有一定的潜伏期,并且潜伏期也具有传染性。如SARS潜伏期一般为2-10天,乙脑的潜伏期为4-21天,新冠肺炎(COVID-19)的潜伏期为7-14天。通常情况下,接触过患病者的人首先会成为没有明显症状的感染者,即潜伏者(Exposed),然后部分潜伏者会转化为患病者,假设潜伏者具有传染性。针对此类传染病,接下来建立SEIR模型
模型假设
- 假设总人数 N 保持不变,人群分为易感者、潜伏者、患病者和病愈免疫的康复者。时刻 t 四类人在总人数中所占比例分别记为 S(t)、E(t)、I(t) 和 R(t),则 S(t)+E(t)+I(t)+R(t) = 1 。
- 假设每个患病者每天有效接触的人数为 λ,当患病者与易感者有效接触时,易感者被感染为潜伏者。
- 假设每个潜伏者每天有效接触的人数为 α,当潜伏者与易感者有效接触时,易感者被感染为潜伏者。
- 假设每天转为患病者的潜伏者占潜伏者总数的比例(称为日转阳率)为 β。
- 假设每天被治愈获得终身免疫力的患病者占患病者总数的比例为常数μ。
模型建立
- 每个患病者每天有效接触的人群中易感者人数为,因此每天将有个易感者因接触患病者被感染为潜伏者;
- 每个潜伏者每天有效接触的人群中易感者人数为,因此每天将有个易感者因接触潜伏者被感染为潜伏者;
- 每天有 个潜伏者转为患病者;
- 每天有个患病者被治愈变为康复者。
从 t 到 t+Δt 四类人人数的增量分别为
记 t=0 时四类人的比例分别为 S0、E0、I0 和 R0,则建立模型
此模型无解析解
1.5.3. 建模案例——冰镇西瓜问题
问题描述
【例】在炎炎夏日里,冰镇西瓜是人们最常吃的消暑佳品,很多人在享受冰爽的西瓜的同时,却很少关注这样一个问题:把一个温热的西瓜放入冰箱的冷藏室,多长时间能够冻透(西瓜的中心温度、表皮温度和冷藏室温度保持一致)?
问题分析
根据能量守恒定律与傅里叶定律,建立冰镇西瓜的热传导方程。

傅里叶定律:在导热现象中,单位时间内沿截面法线方向通过单位面积的热量与温度梯度成正比,即
其中,λ 为导热系数,为温度梯度,负号表示热量传递的方向与温度升高的方向相反。
模型假设
- 假设西瓜是一个半径为 R(m)的理想球体,并假设各部分是均匀的,密度记为 ρ(kg/m3)。
- 假设西瓜为无籽西瓜,瓜皮和瓜瓤的导热性能是完全一致的,其导热系数记为 λ(W/(m.K)),比热容记为 Cp (J/(kg.K)) 。
- 假设冰箱冷藏室是一个温度为 T∞的稳定温度场。
- 西瓜放入冷藏室的时刻记为 t=0时刻,假设零时刻西瓜各部分的温度是均匀的,记为 T0 。
- 假设热量只沿西瓜的半径方向从瓜心向瓜皮传递。
- 西瓜与冷藏室内静止冷空气的对流换热系数记为 h( W/(m2.K))。
几点说明:
- 导热系数是指在稳定传热条件下,1m厚的材料,两侧表面的温差为1开氏度(K)或1摄氏度(℃),在单位时间内,通过1平方米面积传递的热量。
- 比热容是指当单位质量物质吸收或放出热量引起温度升高或降低时,温度每升高1K(或1℃)所吸收的热量或每降低1K(或1℃)所放出的热量。
- 稳定温度场是指各点温度不随时间变化的温度场。
- 西瓜与空气的对流换热系数是指当西瓜表面与附近空气温差1K(或1℃)时,在单位时间内,单位面积上通过对流与附近空气交换的热量。
模型建立
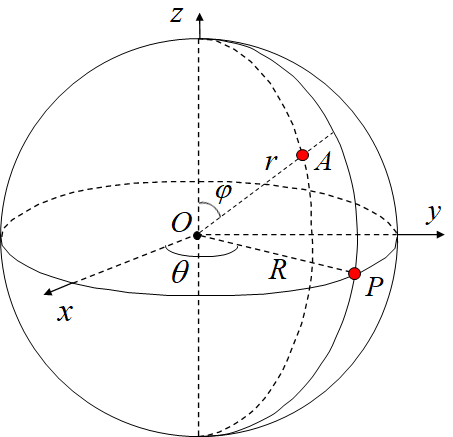
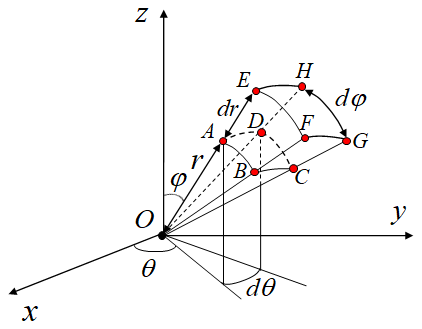
西瓜内任意一点记为 ,在球面坐标系下,考虑由各取得微小增量 所构成的微元体,底面 面积近似为
微元体的体积近似为
dt时间内沿 r 方向从下底面 流入微元体的热量为

从上底面EFGH 流出微元体的热量记为Qr+dr ,则
经 r 方向流入微元体的净热量为
在 dt 时间内,微元体中热力学能的增量(由于微元体温度变化所耗费的能量)为
能量守恒
初值条件:
边值条件:
西瓜表面,单位时间内,通过单位面积从西瓜内部向外流出的热量为
西瓜表面与附近冷空气的温差为 ,在单位时间内,单位面积上通过对流与附近冷空气交换的热量为
热扩散系数:
1. 参数赋值
西瓜初始温度: T0 = 32 ℃,
冰箱冷藏室的温度: T∞ = 6 ℃,
西瓜的半径: R = 9 cm,
西瓜的密度: ρ = 918 kg/m3,
西瓜的导热系数: λ = 0.48 W/(m.K),
西瓜的比热容: Cp = 3990 J/(kg.K),
西瓜与冷藏室静止冷空气的对流换热系数:h = 5 W/(m2.K)。
模型求解
编写初值条件描述函数
function [c,f,s] = pdefun2(r,t,T,dT)
% 冰镇西瓜模型的偏微分方程描述函数
% r --- 距瓜心的距离
% t --- 时间
% T --- 温度
% dT --- 温度T对距离r的偏导
k = 0.48; % 西瓜的导热系数 [w/(m.K)]
p = 918; % 西瓜的密度 [kg/m^3]
Cp = 3990; % 热容 [J/(kg.K)]
a = k/(p*Cp); % 西瓜的热扩散系数 [m^2/s]
c = 1/a; % 标准模型中的c参数
f = dT; % 标准模型中的f参数
s = 0; % 标准模型中的s参数
end
function T0 = pdeic2(r)
% 冰镇西瓜模型的初值条件描述函数
% r --- 距瓜心的距离
T0 = 32; % 西瓜的初始温度
end
function [pa,qa,pb,qb] = pdebc2(ra,Ta,rb,Tb,t)
% 冰镇西瓜模型的边值条件描述函数
% ra,rb --- 下边界和上边界条件中的r值
% Ta,Tb --- 下边界和上边界条件中的T值
% t --- 时间
% pa,pb --- 下边界和上边界条件中的p函数值
% qa,qb --- 下边界和上边界条件中的q函数值
h = 5; % 西瓜与静止冷空气的对流换热系数 [w/(m^2.K)]
Tinf = 6; % 终极温度 [℃],即冰箱冷藏室温度
k = 0.48; % 西瓜的导热系数 [w/(m.K)]
pa = 0;
qa = 1;
pb = h*(Tb - Tinf);
qb = k;
end
调用pdepe函数求解模型
>> m = 2; % 方程中的m参数
>> r = linspace(0,9,41)/100; % 定义距离向量r
>> t = linspace(0,10,41)*3600; % 定义时间向量t
>> T = pdepe(m,@pdefun2,@pdeic2,@pdebc2,r,t); % 模型求解
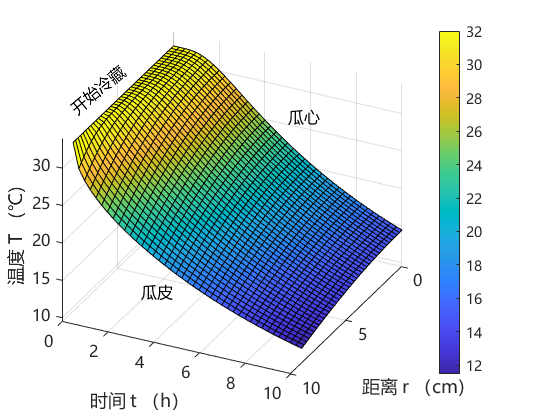
结果可视化
>> figure;
>> surf(r*100,t/3600,T);
>> colorbar;
>> zlim([min(T(:))-2,max(T(:))+2]);
>> xlabel('距离 r (cm)');
>> ylabel('时间 t (h)');
>> zlabel('温度 T (℃)');
>> view(116,33);
>> text(8,-0.5,34.5,'开始冷藏','Rotation',40);
>> text(0,5,26,'瓜心');
>> text(7,2,10.5,'瓜皮');
西瓜等效切面温度扩散动画
>> theta = linspace(0,2*pi,61);
>> X = 100*r'*cos(theta);
>> Y = 100*r'*sin(theta);
>> Ti = T(1,:)'*ones(size(theta));
>> xmin = min(X(:))-1;
>> xmax = max(X(:))+1;
>> ymin = min(Y(:))-1;
>> ymax = max(Y(:))+1;
>> X_bac = linspace(xmin,xmax,50);
>> Y_bac = linspace(ymin,ymax,50);
>> [X_bac,Y_bac] = meshgrid(X_bac,Y_bac);
>> figure;
>> Tinf = 6;
>> surf(X_bac,Y_bac,Tinf*ones(size(X_bac)),'FaceColor','interp','EdgeColor','k');
>> hold on;
西瓜等效切面温度扩散动画
% 绘制零时刻西瓜等效温度切面
>> hs = surf(X,Y,Ti,'FaceColor','interp','EdgeColor','k');
>> axis equal;
>> axis([xmin,xmax,ymin,ymax])
>> xlabel('X'); ylabel('Y');
>> caxis([Tinf,max(T(:))]);
>> colorbar; view(2);
>> ht = title(['冷藏 ',num2str(t(1)/3600,'%2.1f'),' 小时']);
% 通过循环绘制各时刻西瓜等效温度切面
>> for i = 2:numel(t)
Ti = T(i,:)'*ones(size(theta));
set(hs,'ZData',Ti);
set(ht,'String',['冷藏',num2str(t(i)/3600,'%2.1f'),'小时']);
pause(0.2);
end