1.1. 矩阵的创建

MATLAB各种数据类型都是以矩阵形式存在，大部分运算都是基于矩阵运算，矩阵主要分为三类：数值矩阵，符号矩阵和特殊矩阵

1.1.1. 直接创建

MATLAB语言最简单的创建矩阵方法是通过键盘在命令窗口直接输入矩阵，直接输入法的规则是：将所有矩阵元素置于一对方括号“[ ]”内；同一行不同元素之间用逗号“，”或者空格符来分隔；不同行用分号“；”或者回车符分隔。

例如，在命令空间输入：

>> A=[1 2;3 4]       %元素之间用空格符分隔，换行用分号
A =    1     2
    3     4

MATLAB语言创建复数矩阵，方法和创建一般实数矩阵一样，虚数单位用i或者j表示。

例如，创建复数矩阵：

>> B=[1+2i,2-3*j;2+2*sqrt(-2),3.5j]
B =
   1.0000 + 2.0000i   2.0000 - 3.0000i
   2.0000 + 2.8284i   0.0000 + 3.5000i

其中：

虚部和虚数单位之间可以使用乘号“”连接，也可以忽略乘号“”；
复数矩阵元素可以用运算表达式；虚数单位用i或者j，显示时都是i。

1.1.2. 冒号生成矩阵

利用冒号“：” 产生步长相等的一维数组或行向量。
- 其格式为：x=a:step:b a是数组或者行向量的第一个元素，b是最后一个元素，step是步长增量；
冒号表达式可以产生一个由a开始到b结束，以步长step自增或自减（步长为负值，b<a）的数组或者行向量；如果步长step=1，则冒号表达式可以省略步长，直接写为 x=a:b

>> x1=1:1:10
x1 =     1     2     3     4     5     6     7     8     9    10
>> x2=1:10
x2 =     1     2     3     4     5     6     7     8     9    10
>> x3=10:-2:0
x3 =    10     8     6     4     2     0

1.1.3. 利用函数生成矩阵

`linspace`函数

可以用linspace函数生成初值、终值和元素个数已知的一维数组或者行向量，元素之间是等差数列。其
- 调用格式如下：x=linspace(a,b,n)
- a和b分别是生成一维数组或者行向量的初值和终值，n是元素总数。当n省略时候，自动产生100个元素；
- linspace函数产生的一维数组或者行向量，n个元素是等差数列；
- 当a>b,元素之间是等差递减；当a<b，元素之间是等差递增；显然，linspace(a,b,n)与a: (b-a)/(n-1): b是等价的。

>> x1= linspace(0,10,5)
x1 =     0    2.5000    5.0000    7.5000   10.0000
>> x2= linspace(10,0,5)
x2 =   10.0000    7.5000    5.0000    2.5000       0
>> x3=10:(0-10)/(5-1):0
x3 =10.0000   7.5000    5.0000    2.5000       0

logspace函数

MATLAB语言可以用logspace函数生成一维数组或者行向量，元素之间也是对数等比数列。
- 其调用格式如下：
  - x=logspace(a,b,n)
  - 其中：第一个元素为10^a，最后一个元素为10^b，元素个数为n的对数等比数列；如果b的值为pi，则该函数产生到pi之间n个对数等比数列。

>> x1= logspace(1,2,10)
x1 =   10.0000   12.9155   16.6810   21.5443   27.8256   35.9381   46.4159   59.9484   77.4264  100.0000
>> x2= logspace(1,pi,10)
x2 =  10.0000    8.7928    7.7314    6.7980    5.9774    5.2558    4.6213    4.0634    3.5729    3.14164、利用文本文件生成矩阵

1.1.4. 利用文本文件生成矩阵

矩阵还可以由文本文件生成，即先建立txt数据文件，然后在命令窗口直接调用该文件，就能产生数据矩阵。

需要注意，txt文件中不含变量名称，文件名为矩阵变量名，每行数值个数相等。优点：可以将数据存储在文本文件中，利用load函数，直接将数据读入工作空间中，自动生成矩阵，而不需要手动输入数据。

【例】利用文本文件建立矩阵A，其中把下面代码另存为工作目录中，文件名为A.txt文件。

1 2
3 4
>> load A.txt 
>> AA =     1     2     3     4

1.1.5. 利用M文件生成矩阵

对于一些比较大的常用矩阵，可以立一个M文件，在命令窗口中调用文件，适合大型矩阵创建，便于修改。需要注意，M文件中的矩阵变量名不能与文件名相同，否则变量名和文件名会混乱。

%定义example.m函数，将下面代码另存为工作目录下的
A= [34 32 30 28 26 24   
    32 30 28 26 24 22   
    30 28 26 24 22 20   
    28 26 24 22 20 18   
    26 24 22 20 18 16]
>> example
A =  34    32    30    28    26    24
    32    30    28    26    24    22
    30    28    26    24    22    20
    28    26    24    22    20    18
    26    24    22    20    18    16

1.1.6. 特殊矩阵的生成

MATLAB语言中内置了许多特殊矩阵的生成函数，可以通过这些函数自动生成具有不同特殊性质的矩阵。

下表是MATLAB语言常见特殊矩阵函数。

函数名	功能	函数名	功能
eye	单位矩阵	rand	元素服从0~1分布的随机矩阵
zeros	元素全为零的矩阵	randn	元素服从0均值单位方差正太分布的随机矩阵
ones	元素全为1的矩阵	diag	对角矩阵
magic	魔方矩阵	tril(u)	tril下三角矩阵；triu上三角矩阵

单位矩阵

MATLAB语言生成单位矩阵的函数是eye，其调用格式如下：

A1=eye(n);

A2=eye(m,n)。

其中：

A1=eye(n)表示生成的单位矩阵；

A2=eye(m,n)表示生成的单位矩阵。

>> A1=eye(3)
A1=  
         1     0     0
         0     1     0
         0     0     1
>> A2=eye(2,3)
A2 =
     1     0     0
     0     1     0

0矩阵

MATLAB语言生成所有元素为0的矩阵函数是zeros，其调用格式如下：

A1=zeros(n);

A2=zeros(m,n)

其中：

A1= zeros(n)表示生成n*n 的0矩阵；

A2=zeros(m,n)表示生成 m*n的0矩阵；

>> A1=zeros(3)
A1 =      0     0     0
         0     0     0
         0     0     0
>> A2=zeros(1,3)
A2=  0     0     0

1矩阵

MATLAB语言生成所有元素为1的矩阵函数是ones，其调用格式如下：

A1=ones(n);

A2=ones(m,n)。

其中：A1= ones(n)表示生成nn 的1矩阵；A2=ones(m,n)表示生成m\n 的1矩阵。

>> A1=ones(3)
A1=       1     1     1
         1     1     1
         1     1     1
>> A2=ones(2,3)
A2 =    1     1     1
        1     1     1

魔方矩阵

魔方矩阵是指行、列、正和反斜对角线元素之和都相等的矩阵，MATLAB语言用magic函数生成魔方矩阵

其调用格式如下：

A=magic(n)

其中，A=magic(n)表示生成 n*n的魔方矩阵，n>0 且 n不等于2

例如：

>> A=magic(3)A = 8     1     6       3     5     7       4     9     2
>> B=sum(A)     
%计算每列的和
B =    15    15    15
>> C=sum(A')     
%计算每行的和
C =    15    15    15

显然，由B和C结果可知，矩阵A是一个魔方矩阵

0~1均匀分布随机矩阵

MATLAB语言生成0~1均匀分布的随机矩阵函数是rand，其调用格式如下：

A1= rand(n)

表示生成 n*n个元素值为0~1均匀分布的随机矩阵；

A2= rand(m, n)

表示生成m*n 个元素值为0~1均匀分布的随机矩阵；

A3=a+(b-a)*rand(m,n)

表示生成m*n 个元素值为a~b均匀分布的随机矩阵。

>> A1=rand(3)
A1 = 0.8147    0.9134    0.2785
         0.9058    0.6324    0.5469
         0.1270    0.0975    0.9575
>> A3 = 10 + (15 - 10)*rand(2,3) 
A3 = 10.7094   14.5787   14.7975
         12.1088   13.9610   13.2787

正态分布随机矩阵

MATLAB语言生成均值为0，单位方差的正态分布的随机矩阵函数是randn，其调用格式如下：

A1= randn(n)

表示生成 n*n个元素且均值为0，单位方差的正态分布的随机矩阵；

A2= randn(m, n)

表示生成m*n 个元素的正态分布随机矩阵；

A3=a+sqrt(b)*randn(m,n)

表示均值为a，方差为b。

% 例如：
>> A1=randn(3)
A1 = -1.2075    0.4889   -0.3034
        0.7172    1.0347    0.2939
        1.6302    0.7269   -0.7873
>> A3 = 1 + sqrt(0.1)*randn(2,3)  % 均值为1，方差为0.1
A3 =
    1.1028    1.4333    0.9677
    0.7613    0.4588    0.9236

对角矩阵

MATLAB语言生成对角矩阵函数是diag，其调用格式如下：

A=diag(v,k)表示生成以向量v元素作为矩阵A的第k条对角线元素的对角矩阵。

当k=0时，v 为A的主对角线；当k>0时，为主对角线上方第k条对角线元素；

当k<0时，为主对角线下方第k条对角线元素。

例如：

v=[3 2 1];
A1=diag(v)        
A1 = 
     3     0     0          
     0     2     0          
     0     0     1
% 若A是一个矩阵，则diag(A)是提取矩阵A的对角线矩阵。
A=[1 2 3;4 5 6]；
B=diag(A)
B = 1       
    5
>> A2=diag(v,1)
   A2 =    0     3     0     0
           0     0     2     0
           0     0     0     1
           0     0     0     0

三角矩阵

MATLAB语言生成三角矩阵函数是tril和triu，其调用格式如下：

A1=tril(A,k)

表示生成矩阵A中第k条对角线的下三角部分的矩阵；

A1=triu(A,k)

表示生成矩阵A中第k条对角线的上三角部分的矩阵；

其中， k=0为A的主对角线，k>0为A的主对角线以上， k<0为A的主对角线以下。

% 例如：    
>> A=ones(4);
>> L=tril(A,-2)
L =     
    0     0     0     0
    0     0     0     0
    1     0     0     0
    1     1     0     0
>> U=triu(A,0)
U =
     1     1     1     1
     0     1     1     1
     0     0     1     1
     0     0     0     1

1.2. 矩阵的修改

1.2.1. 矩阵部分替换

MATLAB语言可以部分替换矩阵的某个值、某行或者某列的值，常用下面格式：

A(m,n)=a1

表示替换矩阵A中的第m行，第n列元素为a1；

A(m,:)=[a1,a2,...an]

表示替换第m行的所有元素为a1，a2，…，an;

A(:,n)=[a1,a2,…,am]

替换第n列的所有元素为a1，a2，…，am。

% 例如：
>> A=[1 2 3;4 5 6;7 8 9];
>> A(2,:)=[14 15 16] 
A =    
    1     2     3
    14    15    16
    7     8     9
>> A=[1 2 3;4 5 6;7 8 9];
>> A(:,2)=[12 15 18]    %整列替换      
A =
     1    12     3
     4    15     6
     7    18     9

1.2.2. 矩阵部分删除

MATLAB语言可以部分删除矩阵行或者列，常用下面格式：

A(:,n)=[]

表示删除矩阵A的第n列；

A(m,:)=[]

表示删除矩阵A的第m行。

% 例如：
A=[1 2 3 4;2 3 4 5;3 4 5 6] 
A =     
    1     2     3     4
    2     3     4     5
    3     4     5     6

A(2,:)=[]    %删除A的第2行
A =     
    1     2     3     4
    3     4     5     6
>> A(:,2)=[]     %删除A的第2列
A =
     1     3     4
     2     4     5
     3     5     6

1.2.3. 矩阵部分扩展

部分扩展矩阵

生成大的矩阵,常用下面格式：

M=[A; B C]

其中：A为原矩阵，B和C为要扩展的元素，M为扩展后的矩阵；

需要注意，B和C的行数都要相等；

B和C的列数之和要与A的列数相等。

例如：

>>A=[1 0 0 0;0 1 0 0]
A =     
1     0     0     0
0     1     0     0
>>B=zeros(2)；
>>C=eye(2);
>> M=[A;B C]
M =
     1     0     0     0
     0     1     0     0
     0     0     1     0
     0     0     0     1

平铺矩阵函数

MATLAB语言可以利用平铺矩阵函数repmat扩展矩阵，函数调用格式如下：

M=repmat(A,m,n)

其中，M=repmat(A,m,n)表示将矩阵A复制扩展为块。

例如：

>> A=[1 2 3;4 5 6;7 8 9];
>> M=repmat(A,2,3)
M =     
    1     2     3     1     2     3     1     2     3
    4     5     6     4     5     6     4     5     6
    7     8     9     7     8     9     7     8     9
    1     2     3     1     2     3     1     2     3
    4     5     6     4     5     6     4     5     6
    7     8     9     7     8     9     7     8     9

指定维数拼接函数

利用指定维数拼接函数cat拼接矩阵，函数调用格式如下：

M1=cat(1,A,B) 垂直拼接；

M2=cat(2,A,B) 水平拼接；

M3=cat(3,A,B) 三维拼接。

例如：

>> A=eye(2);
>> B=zeros(2);
>> M1=cat(1,A,B)
M1 =     
    1     0
    0     1
    0     0
    0     0
   >> M2=cat(2,A,B)
M2 =
     1     0     0     0
     0     1     0     0
>> M3=cat(3,A,B)
M3(:,:,1) =
     1     0
     0     1
M3(:,:,2) =
     0     0
     0     0

矩阵结构变换

上下行对调可以用函数flipud

上下变换矩阵的结构。

M=flipud(A)

其中M=flipud(A)表示将矩阵A的行元素上下对调，列数不变。

左右列对调可以用函数fliplr左右变换矩阵的结构。

M=fliplr(A)

其中M=fliplr(A)表示将矩阵A的列元素左右对调，行数不变。

例如：

>> A=[1 2 3;4 5 6]
    A =  1     2     3
         4     5     6
>> M=flipud(A)
M =
         4     5     6
         1     2     3
>> A=[1 3 6;2 4 8]
A =     1     3     6
        2     4     8
>> M=fliplr(A)
M =    6     3     1
       8     4     2

3.逆（顺）时针旋转

MATLAB语言可以用函数rot90旋转矩阵的结构，函数调用格式如下：

M1=rot90(A)

表示将矩阵A逆时针旋转90度；

M2=rot90(A,k)

表示将矩阵A旋转k*90度，当k>0, 逆时针旋转，当k<0，顺时针旋转。

例如：

>> A=[1 2 3;4 5 6]
A =     
    1     2     3
    4     5     6
>> M1=rot90(A)
M1 =     
    3     6     2
    5     1     4
>> M1=rot90(A,-1)
M1 =
     4     1
     5     2
     6     3

转置矩阵的转置

用'运算符，调用格式如下：

M1=A’;

M2=B’

其中：当A为实数矩阵时候，转置的运算规则是，矩阵的行变列，列变行；

当B为复数矩阵时候，转置的运算规则是，先将B取共轭，然后行变列，列变行，也就是Hermit转置。

例如：

>> A=[1 2;3 4]
A =
    1     2
    3     4
>> M1=A'
M1 =     
    1     3
    2     4
>> B=[1+i, 1-2i;2+i,2i]
B =   1.0000 + 1.0000i   1.0000 - 2.0000i
        2.0000 + 1.0000i   0.0000 + 2.0000i
>> M2=B'
M2 =  1.0000 - 1.0000i   2.0000 - 1.0000i
      1.0000 + 2.0000i   0.0000 - 2.0000i

5.矩阵的变维

MATLAB语言可以用函数reshape实现矩阵变维，函数调用格式如下：

M=reshape(A,m,n)

其中M=reshape(A,m,n)表示以矩阵A的元素构成 m*n 维M矩阵。显然M中元素个数与A相同。

例如：

>> A=1:8
A =     
    1     2     3     4     5     6     7     8
>> M=reshape(A,2,4)
M =     
        1     3     5     7
        2     4     6     8

1.3. 矩阵的基本运算

1.3.1. 矩阵的加减运算

两个矩阵相加或相减运算的规则是两个同维（相同的行和列）的矩阵对应元素相加减。

若一个标量和一个矩阵相加减，规则是标量和所有元素分别进行相加减操作。加减运算符分别是“+”，“-”。

例如：

>> A=[1 2 3;4 5 6];
>> B=[2 3 4;5 6 7];
>> M1=A-1
M1 =      
    0     1     2
    3     4     5
>> M2=A-B
M2 =
    -1    -1    -1
    -1    -1    -1

1.3.2. 矩阵的乘法运算

两个矩阵相乘运算的规则是第一个矩阵的各行元素分别与第二个矩阵各列元素对应相乘并相加。

假定两个矩阵
$\forall A_{m \times n} B_{n\times p} \rightarrow M = A\times B$ 若一个标量和一个矩阵相乘，规则是标量和所有元素分别进行乘操作。乘法运算符是“*”。

例如：

>> A=[1 2 3;4 5 6];
>> B=[1 2;3 4;5 6];
>> M1=A*B
M1 =    
    22    28    49    64
>> M2=A*2
M2 =
     2     4     6
     8    10    12

1.3.3. 矩阵的除法运算

在MATLAB语言中，有两种除法运算：左除和右除。左除和右除的运算符分别是“\”和“/”。

>> A=[1 2;3 4];
>> B=[1 3;2 1];
>> M1=A\B
M1 =
         0   -5.0000
    0.5000    4.0000

>> M2=B/A
M2 =
    2.5000   -0.5000
   -2.5000    1.5000

1.3.4. 矩阵的乘方运算

在MATLAB语言中，当A是方阵，n为大于0的整数时，一个矩阵A的n次乘方运算可以表示成为A^n，即A自乘n次；当n为小于0的整数时，A^n表示A的逆矩阵（A^-1）的|n|次方。

例如：

>> A=[1 2;3 4];
>> M1=A^2
M1 =     7    10    15    22
>> M2=A^-2
M2 =    
    5.5000   -2.5000   -3.7500    1.7500
>> M=M1*M2
M =
    1.0000    0.0000
   -0.0000    1.0000

显然，由例题可以验证：M=A^2*A^-2=I 单位矩阵。

1.3.5. 矩阵的点运算

点运算是在有关算术运算符前加点。点运算符有“.*”, “./” , “.\” ,“.^”这四种。

点运算规则是对应元素进行相关运算：

若两个矩阵A，B进行点乘运算，要求矩阵维度相同，对应元素相乘；

如果A，B两个矩阵同维，则A./B表示A矩阵除以B矩阵的对应元素；

B.\A表示A矩阵除以B矩阵的对应元素，等价于A./B；

若A，B两个矩阵同维，则A.^B表示两个矩阵对应元素进行乘方运算；

若b是标量，则A.^b表示A的每个元素与b做乘方运算；若a是标量，则a.^B表示a与B的每个元素进行乘方运算。

% 例如：
>> A=[1 2;3 4];
>> B=[1 -1;2 1];
>> C=A.*B     % A点乘B
C =     1    -2
        6     4
>> C=A./B     % A点右除B
C =
      1.0000   -2.0000
      1.5000    4.0000
>> C=B.\A     % B点左除A  
C =
      1.0000   -2.0000
      1.5000    4.0000
>> C=A.^B     %A点乘方B
C =
     1.0000    0.5000
     9.0000    4.0000
>> a=2;b=2;
>> C=A.^b      %A点乘方标量b
C =
     1     4
     9    16
>> C=a.^B      %标量a点乘方B
C =
    2.0000    0.5000
    4.0000    2.0000

点运算有时候点运算可以代替一重循环运算，例如：当x从0到1，增量是0.1变化，求函数的值。一般需要用一重循环语句，求出y的值。而用MATLAB语言的点运算，可以很方便求出y的值，具体代码如下：

>> x=0:0.1:1
x = 
0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000   0.9000   1.0000
>> y=exp(x)*sin(x)

错误使用 * 内部矩阵维度必须一致。

>> y=exp(x).*sin(x)
y = 
0    0.1103    0.2427    0.3989    0.5809    0.7904    1.0288    1.2973    1.5965  
1.9267    2.2874

其中，y表达式中必须用点乘运算，因为exp(x)和sin(x)是一个1同维的矩阵。

% 例如：
>> A=[1 2;3 4];
>> B=[1 -1;2 1];
>> C=A.*B     % A点乘B
C = 1    -2
       6     4
>> C=A./B     % A点右除B
C =1.0000   -2.0000
      1.5000    4.0000
>> C=B.\A     % B点左除A  
C =1.0000   -2.0000
      1.5000    4.0000
>> C=A.^B     %A点乘方B
C =1.0000    0.5000
     9.0000    4.0000

1.4. 矩阵的分析

方矩阵的行列式

D=det（A）

矩阵的秩和迹

函数求方矩阵A的行列式的值。

1.矩阵的秩

与矩阵线性无关的行或者列数称为矩阵的秩。

r=rank（A）函数求矩阵的秩

2.矩阵的迹

矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和

t=trace（A）函数求矩阵的迹

% 例如：
>> A=[1 0 1; 2 1 0; 0 2 1]；
>> D=det(A)
D =
    5
>> r=rank(A)
r = 
    3
>> t=trace(A)
t = 
    3

矩阵的逆和伪逆

1.方阵的逆矩阵

在MATLAB语言里，用求逆矩阵的函数是inv(A)。

例如：

>> A=[1 0 1;2 1 0;0 2 1]
A =  
    1     0     1
    2     1     0
    0     2     1
>> B=inv(A)
B =    
    0.2000    0.4000   -0.2000
    -0.4000   0.2000    0.4000
    0.8000   -0.4000    0.2000
>> A*B
ans =
     1     0     0
     0     1     0
     0     0     1
>> B*A
ans =
     1     0     0
     0     1     0
     0     0     1

显然，AB=BA=I, 故B与A是互逆矩阵。

2.矩阵的伪逆矩阵

如果矩阵A不是一个方阵，或者A为非满秩矩阵，那么就不存在逆矩阵，但可以求广义上的逆矩阵B，称为伪逆矩阵。

MATLAB语言用B=pinv(A)函数求伪逆矩阵。

例如：

>> A=[1 0 1;2 1 0]
A =     
        1     0     1     
        2     1     0
>> B=pinv(A)
B =    
    0.1667    0.3333   -0.3333
    0.3333    0.8333   -0.3333

在线性代数中，可以用矩阵求逆的方法求解线性方程组的解。将设有n个未知数，由n个方程构成线性方程组，表示为： $\begin{cases}a_{11}x_{1} +a_{12}x_{2}+...+a_{1n}x_{n}=b_{1}\\a_{21}x_{1} +a_{22}x_{2}+...+a_{2n}x_{n}=b_{2}\\ ...\\ a_{n1}x_{n} +a_{12}x_{2}+...+a_{nn}x_{n}=b_{n}\\ \end{cases}$ 用矩阵表示为： $Ax=b$

其中：线性方程组的解为： $A =\left[\begin{matrix} a_{11} & a_{12} & ... & a_{1n}\\ a_{21}& a_{22}&...&a_{2n}\\ ...&...&...&...\\ a_{n1}&a_{n2}&...&a_{nn} \end{matrix}\right], x = \left[\begin{matrix} x_{1} \\ x_{2}\\...\\ x_{n} \end{matrix} \right], b = \left[\begin{matrix} b_{1} \\ b_{2} \\ ... \\ b_{n} \end{matrix}\right]$ 线性方程组的解为： $x=A^{-1}b$ 所以，求系数矩阵A的逆矩阵，可以求线性方程组的解。

【例】利用MATLAB求系数矩阵的逆矩阵方法，求下列线性方程组的解。 $\begin{cases} x-y+z = 3 \\ 3x+y - z = 6 \\ x+y+z = 4 \end{cases}$ MATLAB命令程序如下：

A=[1 -1 1;3 1 -1;1 1 1];
b=[3; 6; 4];
x=inv(A)*b
x =    
    2.2500    0.5000    1.2500

矩阵的特征值和特征向量

求矩阵的特征值和特征向量用eig(A)函数，常用下面两种格式：

E=eig(A)：求矩阵A的特征值，构成向量E；
[v,D]=eig(A) 求矩阵A的特征值D和特征向量v。

% 例如：
>> A=[1 1 1;1 0 0.25;0.5 0.25 2];
>> [v,D]=eig(A)
v =        0.5334   -0.6834    0.6435
        -0.8456   -0.5326    0.3174
        -0.0211    0.4992    0.6966
D =       -0.6246         0         0
              0    1.0488         0
              0         0    2.5758
>> A*v
ans =   -0.3332   -0.7168    1.6574
           0.5282   -0.5586    0.8176
           0.0132    0.5236    1.7942
>> v*D
ans =     -0.3332   -0.7168    1.6574
         0.5282   -0.5586    0.8176
         0.0132    0.5236    1.7942

显然，Av= vD，故D和v分别是A矩阵的特征值和特征向量。

特征值还应用求解一元多次方程的根，具体方法是，先将方程的多项式系数组成行向量a，然后用compan(a)函数构造成伴随矩阵A，最后再用eig(A)函数求A的特征值，特征值就是方程的根。

【例】用MATLAB求特征值的方法求解一元多次方程的根，方程如下： $x^{5}-5x^{4}+5x^{3}+5x^{2}-6x=0$

% MATLAB命令程序如下：
a=[1 -5 5 5 -6 0];
A=compan(a);
x1=eig(A)
x1 =   0
    3.0000
   -1.0000
    2.0000
    1.0000
% 求一元多次方程的根还可以利用多项式函数roots。
x2=roots(a)
x2 =  0
    3.0000
   -1.0000
    2.0000
    1.0000

显然，用这两种不同方法求解一元多次方程的根，结果是一样的。

矩阵的分解

1.对称正定矩阵分解

对称正定矩阵Cholesky分解用函数chol(A), 函数语法格式如下：

[R,p]=chol(A)，其中分解后的R满足R’*R=A。

若A是n阶对称正定矩阵，则R为实数的非奇异上三角矩阵，p=0；

若A是非正定矩阵，则p为正整数。

例如：已知A=[1 1 1;1 2 3;1 3 6],求该矩阵的Cholesky分解

MATLAB语言程序代码及结果如下：

>> A=[1 1 1;1 2 3;1 3 6];
>> [R,p]=chol(A) 
R =     
    1     1     1 
    0     1     2
    0     0     1
p = 
    0
>> R'*R
ans =
     1     1     1
     1     2     3
     1     3     6

2.矩阵的高斯消去法

分解lu（A）函数实现LU分解。

函数语法格式如下：

[L,U]=lu(A)，其中L为下三角矩阵或其变换形式，U为上三角矩阵，且满足LU=A；[L,U，P]=lu(A)，

其中L为下三角矩阵，U为上三角矩阵，P为单位矩阵的行变换矩阵，且满足LU=PA。

例如：已知A=[1 2 3;4 5 6;7 8 9],求该矩阵的LU分解。

>> A=[1 2 3;4 5 6;7 8 9];
>> [L,U]=lu(A)
L =    0.1429    1.0000         0
       0.5714    0.5000    1.0000    
       1.0000         0         0
U =   7.0000    8.0000    9.0000
         0      0.8571    1.7143
         0      0           -0.0000
>> L*U
ans =  
        1     2     3
        4     5     6
        7     8     9

LU分解得到的L是一个下三角变换矩阵，U是一个上三角矩阵，且满足L*U=A。

3.矩阵的正交分解

Qr(A)函数实现QR分解。

函数语法格式如下：

[Q,R]=qr(A)，其中Q为正交矩阵，R为上三角矩阵，满足QR=A；
[Q,R,E]=qr(A)，其中Q为正交矩阵，R为对角元素按大小降序排列上三角矩阵，E为单位矩阵的变换形式，且满足QR=AE。

例如：已知A=[1 2 3;4 5 6;7 8 9],求该矩阵的QR分解。

>> A=[1 2 3;4 5 6;7 8 9];
>> [Q,R]=qr(A)
Q = 
    -0.1231    0.9045    0.4082
    -0.4924    0.3015   -0.8165       
    -0.8616   -0.3015    0.4082
R = -8.1240   -9.6011  -11.0782
     0         0.9045    1.8091
     0         0        -0.0000

QR分解得到的Q是一个正交矩阵，R是一个上三角矩阵，且满足Q*R=A。

例如：已知A=[1 2 3;4 5 6],求该矩阵的奇异值分解。

>> A=[1 2 3;4 5 6];
>> [U,S,V]=svd(A)
U =   -0.3863   -0.9224 
      -0.9224    0.3863
S =    9.5080         0         0 
            0    0.7729         0
V =  -0.4287    0.8060    0.4082
        -0.5663    0.1124   -0.8165
        -0.7039   -0.5812    0.4082
>> U*S*V'
ans = 
          1.0000    2.0000    3.0000
          4.0000    5.0000    6.0000

奇异值分解得到的一个与A同大小的对角矩阵S，两个酉矩阵U和V，且满足A= USV'。

矩阵的信息获取函数

1.Size

size(A)函数来获取矩阵A的行和列的数。

调用格式如下所示：

D=size(A)，返回一个行和列数构成两个元素的行向量；

[M,N]=size(A)，返回矩阵A的行数为M，和列数为N。

2.length

length(A)函数获取矩阵A的行数和列数的较大者，调用格式为d=length(A)，返回矩阵A的行数和列数的较大者。

3.numel

numel(A)函数来获取矩阵A的元素总个数。

调用格式为：n=numel(A)，返回矩阵A的元素总个数。

>> A=[1 2 3;4 5 6]
>> D=size(A)
D =     
    2     3
>> [M,N]=size(A)
M =  
    2
N =  
    3
>> d=length(A)
d =  3
>> n=numel(A)
n =  6

1.5. 字符串

字符串的创建

字符串一般以ASCII码形式存储，以行向量形式存在，并且每个字符占用两个字节的内存。

创建一个字符串有下面几种方法：

1）直接将字符内容用单引号（' '）括起来

2）用方括号连接多个字符串组成一个长字符串

>> str='Student_name'
str =Student_name
>> whos
    Name      Size            Bytes  Class    Attributes 
    Str       1x12               24  char

若要显示单引号（'）字符，需要使用两个单引号，例如：

>> str='I''m a student'
str =
    I'm a student
>> str=['I''m' ' a' ' student']
str =
    I'm a student

3）用函数strcat把多个字符串水平连接合并成一个长字符串。

str=strcat(str1,str2,…)

>> str1='I''m a student';
>> str2= ' of';
>> str3=' Guangdong Ocean University';
>> str=strcat(str1,str2,str3)
str =
    I'm a student of Guangdong Ocean University

4）用函数strvcat把多个字符串连接成多行字符串。

str=strvcat(str1,str2,…)

>> str1='good';
>> str2='very good';
>> str3='very very good';
>> strvcat(str1,str2,str3)
ans =
    good          
    very good     
    very very good

abs或者double函数获取字符串所对应的ASCII码数值矩阵。相反，可以用char函数把ASCII码转换为字符串。

例如

>> str1=‘I’’m a student’ ;
>> A=abs(str1)     %把字符串转换为对应的ASCII码数值矩阵
A = 73    39   109    32    97    32   115   116   117   100   101   110   116
>> str=char(A)    %把ASCII码数值矩阵转换为字符串str =I'm a student

【例】已知一个字符串向量str='It is a Green Bird'，完成以下任务：

1）计算字符串向量字符个数；

2）显示‘a Green Bird’

3）将字符串倒序重排

4）将字符串中的大字母变成相应小写字符，其余字符不变。

str='It is a Green Bird'   %创建字符串向量
n=length(str)                % 计算字符串向量字符个数
str1=str(7:18)               % 显示‘a Green Bird’
str2=str(end:-1:1)          % 将字符串倒序重排
k=find(str>='A'&str<='Z') % 查找大写字母的位置
str(k)=str(k)+('a'-'A')    % 将大写字符变成相应小写字母
% 程序运行结果如下：
str =It is a Green Bird
n =    18
str1 =a Green Bird
str2 =driB neerG a si tI
k =     1     9    15
str =it is a green bird

字符串的操作

1.字符串比较

MATLAB语言比较两个字符串是否相同的常用函数有四个：

strcmp、strncmp、strcmpi和strncmpi，字符串比较函数的调用格式及功能说明如表所示。

函数名	调用格式	功能说明
strcmp	strcmp(str1,str2)	比较两个字符串是否相等，相等为1，不等为0
strncmp	strncmp(str1,str2,n)	比较两个字符串前n个字符是否相等，相等为1，不等为0
strcmpi	strcmpi(str1,str2)	忽略大小写，比较两个字符串是否相等，相等为1，不等为0
strncmpi	strncmpi(str1,str2,n)	忽略大小写，比较两个字符串前n个字符是否相等，相等为1，不等为0

2.字符串查找和替换

MATLAB语言查找与替换字符串常用函数有五个：

strfind、findstr、strmatch、strtok和strrep，字符串查找函数的调用格式及功能说明如表所示。

函数名	功能说明
strfind(str, 'str1')	在字符串str中查找另一个字符串str1出现的位置
findstr(str, 'str1')	在一个较长符串str中查找较短字符串str1出现的位置
strmatch('str1',str)	在str字符串数组中，查找匹配以字符str1为开头的所在的行数
strtok(str)	从字符串str中截取第一个分隔符（包括空格，Tab键，回车键）前面的字符串
strrep(str,'oldstr','newstr')	在原来字符串str中，用新的字符串newstr替换旧的字符串oldstr

3.字符串的其他操作

在MATLAB语言中，除了常用的字符串创建、比较、查找和替换操作外，还有许多其他字符串操作，如表所示。

函数名	函数功能及说明
upper(str)	将字符串str中的字符转为大写
lower(str)	将字符串str中的字符转为小写
strjust(str,’right ’)strijust(str)	将字符串str右对齐
strjust(str,’left ’)	将字符串str左对齐
strjust(str,’center ’)	将字符串str中间对齐
strtrim(str)	删除字符串开头和结束的空格符
eval(str)	执行字符常量str运算

字符串转换

在MATLAB语言中，字符串进行算术运算，会自动转换为数值型。提供许多字符串与数值之间转换函数，如表所示。

函数名	格式及例子	功能与说明
abs	abs('a')=97	将字符串转换为ASCII码数值
double	double('a')=97	将字符串转换为ASCII码数值的双精度数据
char	char(97)=a	将数值整数部分转换为ASCII码等值的字符
str2num	str2num('23')=23	将字符串转为数值
num2str	num2str(63)= '63'	将数值转为字符串
str2double	str2double('97')=97	将字符串转为双精度类型数据
mat2str	mat2str([32,64;97,101])=' [32 64;97 101] '	将矩阵转为字符串
dec2hex	dec2hex(64)= '40'	将十进制整数转为十六进制整数字符串
hex2dec	hex2dec ('40')=64	将十六进制字符串转为十进制整数
dec2bin	dec2bin(16)= '10000'	将十进制整数转为二进制整数字符串
bin2dec	bin2dec('10000')=16	将二进制字符串转为十进制整数
dec2base	dec2base(16,8)= '20'	将十进制整数转为指定进制整数字符串
base2dec	base2dec('20',8)=16	将指定进制字符串转为十进制整数

1.6. 多维数组

多维数组的创建

多维数组的创建一般有四种方法：

直接赋值法、二维数组扩展法、使用cat函数创建法和使用特殊数组函数法。

直接赋值法
二维数组扩展法
使用函数cat创建法
使用特殊数组函数法

多维数组的操作

1.多维数组元素的提取

2.多维数组形状的重排

3.多维数组维度的重新排序

1.7. 单元数组和元胞数组

单元数组

单元数组又称细胞数组（Cell array），其基本元素是细胞，每个细胞可以存储不同类型、不同维数的数据。

1.单元数组的创建

单元数组中不同位置可有不同数据类型，它可以有数字、字符串组成，其创建方法有：

1)使用大括号{ }直接创建

例如：

>> A={'Command window ','Workspace';'Current Folder','Command History'}   
A =
    'Command window '    'Workspace'             
    'Current Folder'     'Command History'

2)对细胞元素直接赋值创建

【例】创建一个学生的各科成绩单元数组。

>> B{1,1}='语文';  B{1,2}='数学';
B{1,3}='外语';  B{1,4}='物理';  B{1,5}='化学';  B{1,6}='生物';
>> B{2,1}=102;  B{2,2}=125;  B{2,3}=130;  B{2,4}=86;  B{2,5}=82;  B{2,6}=80;
>> B
运行结果如下：
B =     '语文'    '数学'    '外语'    '物理'    '化学'    '生物'  
        [ 102]    [ 125]    [ 130]    [  86]    [  82]    [  80]

3)利用函数cell创建一个大小合适的空矩阵

格式：cell(m,n) %创建一个m×n的空细胞矩阵，矩阵所有行必须要有相同的细胞数该方法

首先使用cell函数定义一个单元数组，此时，由于数组的各个元素还没有定义，因此，所显示的单元数组中元素都用空阵[]来表示。

然后，依次输入单元数据中各个元素的值，可以发现，每输入一个值，用相应的值代替空阵。

【例】创建2×3的细胞数组。

>> C=cell(2,3)
C = 
     []     []     []
     []     []     []
>> C{1,1}='MATLAB'
C = 
    'MATLAB'    []    []
     []         []    []
>> C{1,2}='Matrix'
C = 
    'MATLAB'    'Matrix'    []
     []              []          []
>>  C{1,3}='Laboratory'
C = 
    'MATLAB'    'Matrix'    'Laboratory'
       []             []                []
>> C{2,1}=['12','34';'56','78']
C = 
    'MATLAB'      'Matrix'    'Laboratory'
    [2x4 char]          []              []
>> C{2,2}=[12,34;56,78]
C = 
    'MATLAB'      'Matrix'        'Laboratory'
    [2x4 char]    [2x2 double]              []
>> C{2,3}='矩阵实验室'
C = 
    'MATLAB'      'Matrix'        'Laboratory'
    [2x4 char]    [2x2 double]      '矩阵实验室'

4)单元数组的显示

celldisp函数

格式：celldisp(cell) %逐个显示cell的每个元素的值

例如，对【上例】中的细胞数组C，执行命令：

>> celldisp(C)

显示的结果如下：

C{1,1} =
     MATLAB
C{2,1} =
     1234
5678
C{1,2} =
     Matrix

C{2,2} =
     12    34
     56    78
C{1,3} =
    Laboratory
C{2,3} =
    矩阵实验室

cellplot函数

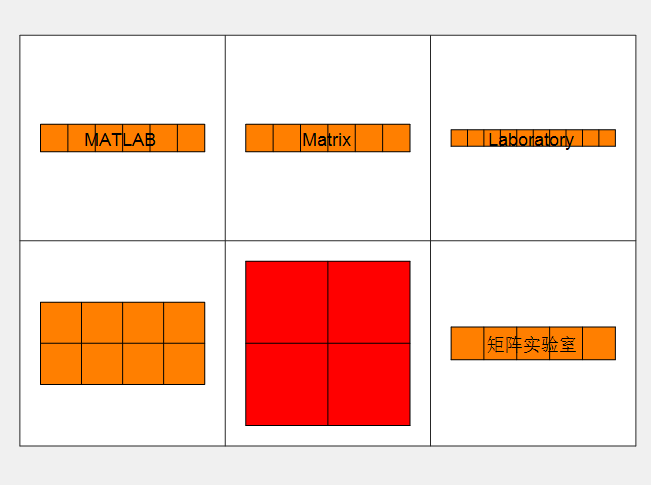
格式：cellplot(C) %用彩色的图形来显示单元型变量C的结构形式例如，

对【上例】中的细胞数组C，继续执行命令：

>> cellplot(C)

显示结果如下图所示。

2 数组体内部数据的获取

为了获取单元数组中一个单元的值，只需使用大括号。

如对【上例】中的数组C，执行命令：

>> C{1}
ans =          
    MATLAB
>> C{2}
ans =
    1234         5678
>> C{3}
ans =
    Matrix

实际上，C{1}相当于C{1,1}；C{2}相当于C{2,1}；C{3}相当于C{1,2}，等等。

注意使用大括号与小括号的不同，大括号是用于标示单元而不考虑这些单元的值，而小括号用于寻址单元的值。

3.结构体的操作函数

MATLAB的单元数组在进行统计分析时，不能直接使用计算统计量的函数，而必须将单元数组中单元的数值转化成数值向量，随后进行数值计算。例如，

对【例3-1】中形成的数组，计算这个学生考试的总分。由于数组B的显示结果为：

B =    
    '语文'    '数学'    '外语'    '物理'    '化学'    '生物'
    [ 102]    [ 125]    [ 130]    [  86]    [  82]    [ 80]

若直接对B的第2行求和，命令窗口显示出错。这时需将单元数组转化成数值数组，具体程序如下：

for i=1:6
X(i)=B{2,i};    %将单元数组C的第二行第i列的内容赋于数值数组X
end
X, sum(X)     %显示数组X及考试总分
% 运行结果如下：
X =
   102   125   130    86    82   80
ans =
   605

元胞数组

结构数组（Structure array）是把一组彼此相关、数据结构相同但类型不同的数据组织在一起，便于管理和引用。类似于数据库，但其数值组织形式更灵活。

1.元胞数组的创建

1)直接输入法

在给结构数组中元素直接赋值的同时定义该元素的名称，并使用“.”将结构变量名与元素名连接。

格式：

struct_name(record#).field_name=data

%创建将数据data直接赋值给变量名

%struct_name(record#)和元素名

%field_name的结构数组

说明：创建1×1的结构数组时可省略记录号(record#)项。

【例3-3】建立学生档案的小型数据库。

>> student.test=[90 86 82 88 92 75 80];
>> student.name='zhaohua';
>> student.sex='F';
>> student.age=20;
>> student.num=20110501;
>> student.add='qd uinversity';
>> student.tel='13905329191';
>> student
运行结果如下：
student = 
     test: [90 86 82 88 92 75 80]
    name: 'zhaohua'
    sex: 'F'
     age: 20
     num: 20110501
     add: 'qd uinversity'
     tel: '13905329191'

2)使用struct函数生成结构数组

格式：

S=struct('field1',V1, 'field2',V2,…)

% field为各成员变量名，V为对应的各成员

%变量的内容，返回结构数组S

【例3-4】用struct函数创建结构数组变量。

>> S =struct('city',{'beijing','shanghai'},'renkou',[1500,1300])
% 运行结果如下：
S = 1x2 struct array with fields:    city    
renkou
>>S.city
ans =
    beijing
ans =
    shanghai
>> S.renkou
ans =
    1500        1300

2.元胞数组的操作

1)在结构数组中添加项如果用户想在一个结构数组中添加其它项，直接按照生成格式输入即可。

2)在结构数组中删除项

格式：

S=rmfield(S,fields)

%将结构数组S中的fields项删去，仍用数组名S表示

说明：当fields是字符串或单元数组变量时，将一次性删除多项。

3)在结构数组中调用元素项结构数组中的任何信息，可以通过“结构体名称+元素项名称”的格式取出。

格式：

C=struct2cell(S)

%将结构数组S转化为单元数组

CS=cell2struct(C)

%将单元数组C转化为结构数组S

例如，在【例3-4】中创建的结构数组S，执行命令：

>> C=struct2cell(S)
C(:,:,1) =  
    'beijing'    [1x2 double]
C(:,:,2) = 
    'shanghai'    [1x2 double]
>> C=[C(:,1),C(:,2)]
C =
    'beijing'       'shanghai'  
    [1x2 double]    [1x2 double]

1.8. 矩阵及其运算应用实例

矩阵在图像处理中应用

【例】已知一幅数字图像lena.bmp，进行左右、上下翻转、逆时针翻转90度、顺时针翻转90度以及图像平铺3*2=6块处理。

A=imread('E:\work\lena.bmp','bmp');  
subplot(2,3,1) 
imshow(A)
title('原始图像')
B=fliplr(A);    
subplot(2,3,2)
imshow(B);
title('左右对调')
C=flipud(A); 
subplot(2,3,3)
imshow(C)
title('上下对调')
D=rot90(A);                             
subplot(2,3,4)
imshow(D)
title('逆时针旋转90度')
E=rot90(A,-1);                          
subplot(2,3,5)
imshow(E)
title('顺时针旋转90度')
F=repmat(A,3,2);                        
subplot(2,3,6)
imshow(F)
title('图像平铺2*3块 ')

线性方程组的求解

1.线性方程组唯一解

用MATLAB语言求解线性方程组唯一解的方法常用左除法和逆矩阵法。

2.线性方程组多解

用MATLAB语言求解线性方程组

多解的方法常用左除法和伪逆矩阵法pinv(A)

【例】在MATLAB语言中，用左除法和伪逆矩阵法分别求解下列线性方法组的解。 $A_{m\times n}x=b$

$\begin{cases} x_{1}-x_{2}+x_{3}+x_{4}= 2\\ 3x_{1}+x_{2}-x_{3}+x_{4} = 6 \\ x_{1}+x_{2}+x_{4}=4 \end{cases}$

>> A=[1 -1 1 1;3 1 -1 1;1 1 0 1];
 >> b=[2 6 4]';
>> r=rank(A)
r =
     3
>> x=A\b                         
x =
    2.0000
    2.0000
    2.0000
         0
>> x=pinv(A)*b                    
 x =
    1.2000
    1.2000
    0.4000
    1.6000

多维数组在彩色图像中应用

彩色图像被读入MATLAB中，RGB三种颜色分量一般被存为三维数组。对彩色图像处理，实际上是对三维数组进行提取和操作，所以用MATLAB语言处理彩色图像比较方便。

【例】用MATLAB语言，对一幅彩色图像，分别提取红色分量，绿色分量和蓝色分量，并在同一个图形窗口不同区域显示，利用cat函数把三个分量连接成一个三维数组，并显示合成后的图像。