1. MATLAB语言符号运算

1.1. MATLAB符号运算的概述

在MATLAB中的命令，如果其操作对象不是数值而是符号（符号表达式或符号数组），相应的计算称为符号计算。例：当a,b是变量时，计算积分就是符号计算。

在符号计算中，通过符号常数、符号变量及有关符号操作形成符号表达式。

MATLAB中符号计算函数是数值计算函数的重载、符号计算工具箱采用的函数和数值计算的函数有一部分同名，为了得到准确的在线帮助，不能直接使用”help 函数名”的格式、而应该使用”help sym/函数名”的格式。

[例]查询逆矩阵符号计算。

help sym/inv
help sym/inv
 inv    Symbolic matrix inverse.
    inv(A) computes the symbolic inverse of A
    inv(VPA(A)) uses variable precision arithmetic.
     Examples:
       Suppose B is
          [ 1/(2-t), 1/(3-t) ]
          [ 1/(3-t), 1/(4-t) ]
        Then inv(B) is
          [     -(-3+t)^2*(-2+t), (-3+t)*(-2+t)*(-4+t) ]
          [ (-3+t)*(-2+t)*(-4+t),     -(-3+t)^2*(-4+t) ]
        digits(10);
       inv(vpa(sym(hilb(3))));

1 符号运算与数值运算的区别

数值运算中必须先对变量赋值，然后才能参与运算。
符号运算无须事先对独立变量赋值，运算结果以标准的符号形式表达。

特点：

运算对象可以是没赋值的符号变量

可以获得任意精度的解

Symbolic Math Toolbox——符号运算工具包通过调用Maple软件实现符号计算的。

maple软件——主要功能是符号运算，它占据符号软件的主导地位

1.2. MATLAB符号对象的创建和使用

1.2.1. Matlab符号矩阵的创建

数值矩阵A=[1,2;3,4]

A=[a,b;c,d] —— 不识别

1）用matlab函数str2sym创建矩阵（symbolic的缩写)

命令格式： A=str2sym('[ ]')

※ 符号矩阵内容同数值矩阵

※ 需用str2sym指令定义

※ 需用' '标识

2）用syms 先定义变量，然后直接

输入矩阵表达式

A=str2sym('[a 2*b;3*a 0] ')
 A =
[   a, 2*b]
[ 3*a,   0]
syms a b
>> B=[a 2*b;3*a 0]
B =
[   a, 2*b]
[ 3*a,   0]

(2)两种定义符号表达式的区别：

f1=str2sym('x^2+1')
f1 =x^2+1
 syms x
f2=x^2+1
f3='x^2+1'
f3 =x^2+1
 >> whos
  Name      Size            Bytes  Class    Attributes
  f1            1x1                112         sym                
  f2            1x1                112         sym                
  f3            1x5                10         char               
  x             1x1               112         sym

3) 基本的符号运算

MATLAB中基本的符号运算范围及所采用的运算符号与数值运算没有大的差异，涉及的运算函数也几乎与数值计算中的情况完全一样，简介如下：
- 算术运算
- 加、减、乘、左除、右除、乘方：＋、－、*、\、/、\^；
- 点乘、点左除、点右除、点乘方：.*、.\、./、.\^ ；
- 共轭转置、转置：′、.′；
关系运算
- 相等运算符号：= =；
- 不等运算符号：~=；
- 符号关系运算仅有以上两种。
三角函数、双曲函数和相应的反函数
- 三角函数：sin、cos和tan等；
- 双曲函数：sinh、cosh和tanh等；
三角函数、双曲函数的反函数
- 反三角函数：asin、acos和atan等；
- 反双曲函数：asinh、acosh和atanh等；
复数函数
求复数的共轭：conj；求复数的实部：real；求复数的虚部：imag
求复数的模：abs；求复数的相角：angle；等等；
矩阵函数
求矩阵对角元素：diag；求矩阵的上三角矩阵：triu；求矩阵的下三角矩阵：tril
求矩阵的逆：inv；求矩阵的行列式：det；
求矩阵的秩：rank
求矩阵的特征多项式：poly；求矩阵的指数函数：expm
求矩阵的特征值和特征向量：eig；求矩阵的奇异值分解：svd

【例】举例说明数值量与符号对象的混合运算。

>> syms a b c
>> B=[a b;c 0] ]     %定义一个符号矩阵B
 B =
 [ a, b]
[ c, 0]
 >> C=inv(B)
 C =
 [   0,      1/c]
[ 1/b, -a/(b*c)]
>> D=[1 2;3 4]；     %定义一个数值矩阵D
D =
     1     2
     3     4
>> C+D           %数值矩阵D与符号矩阵C直接相加
ans =
[       1,     1/c + 2]
[ 1/b + 3, 4 - a/(b*c)]

4) 符号矩阵的修改

a.直接修改

可用、键找到所要修改的矩阵，直接修改

A(*,*)=‘new’

b.指令修改

用A1=subs(A, 'old‘, 'new')来修改

%例如：
A=sym('[a,2*b;3*a,0]') 
A =[    a, 2*b]
 [3*a,     0]
A2=subs(A, 'b’,'c')  
A2 =[    a, 2*c] 
        [3*a, 0]

5). 符号矩阵与数值矩阵的转换

将数值矩阵转化为符号矩阵

函数调用格式：sym(A)

A=[1/3,2.5;1/0.7,2/5]
A =
       0.3333    2.5000
       1.4286    0.4000
sym(A)
ans =
[ 1/3,  5/2]
[10/7, 2/5]

将符号矩阵转化为数值矩阵

可以用double()

A =
[ 1/3, 5/2]
[10/7, 2/5]
double(A)
ans=
    0.3333    2.5000
    1.4286    0.4000

6) 符号函数

(1) 使用符号表达式

[例 ]计算使用符号表达式分别形成符号函数 f=sin(x)cos(y)、g=ln(x2+y2)。

[算例代码]

  clear;
  syms x y;
  f=sin(x)*cos(y)
  g=log(x^2+y^2)

(2)使用m文件

实际编程中，使用编制m文件形成符号函数、然后再行调用，有时候更为方便一些。

function f=f0605
syms x y
f=sin(x)*cos(y)

1.3. MATLAB符号多项式函数运算

1.3.1. 多项式函数的符号表达形式及相互转换

（1）多项式的展开

采用以下的函数指令可以将多项式展开成乘积项和的形式。

g=expand(f)       %将多项式展开成乘积项和的形式

通过输入以下的命令行进行举例说明：

syms x y a b c
>> f1=(x-a)*(x-b)*(x-c) ;
>> f2=a*sin(x+b)+c*sin(x+a) ;
>> g1=expand(f1)          %将多项式f1展开
g1 =
x^3 - b*x^2 - c*x^2 - a*x^2 - a*b*c + a*b*x + a*c*x + b*c*x
>> g2=expand(f2)
 g2 =
 a*cos(b)*sin(x) + a*sin(b)*cos(x) + c*cos(a)*sin(x) + c*sin(a)*cos(x)

（2）多项式的整理

多项式的书写习惯是按照升幂或降幂的规则来完成，否则需要加以整理。上例中g1式子并不符合人们的书写习惯，可以使用下列的函数指令加以整理。

h=collect(g)              %按照默认的变量整理表达式g，
h=collect(g,v)            %按照指定的变量或表达式v整理表达式g

通过输入以下的命令行进行举例说明：

>> h1=collect(g1)         %按照变量x整理表达式g1
h1 =x^3 + (- a - b - c)*x^2 + (a*b + a*c + b*c)*x - a*b*c
>> h2=collect(g2,cos(x))
h2 =
 (a*sin(b) + c*sin(a))*cos(x) + a*cos(b)*sin(x) + c*cos(a)*sin(x)

（3）多项式的因式分解

把一个多项式在一个范围内化为几个整式的积的形式，这种变形叫做因式分解，也称为分解因式。MATLAB所提供的因式分解函数指令格式为：

p=factor(f)                  %将符号对象f进行因式分解

输入以下的命令行进行举例说明：

>> syms x  %声明一个符号变量集
>> f1=x^2-3*x+2;            %定义符号表达式f1
>> h1=factor(f1)               %将f1进行因式分解
h1 =
 [ x - 1, x - 2]

例：当取何值时，齐次线性方程组：有非零解

对于齐次线性方程组，当rank（A）\<n或时，齐次方程组有非零解。程序如下：

syms lamda
A=[1-lamda,-2,4;2,3-lamda,1;1,1,1-lamda];
>> D=det(A)
D =
- lamda^3 + 5*lamda^2 - 6*lamda
factor(D)
ans = 
[ -1, lamda, lamda - 2, lamda - 3]

（4）多项式转换成嵌套形式

在编制多项式计算程序时，如若知道多项式的嵌套形式，那么便可以采用一种迭代的算法来完成多项式的计算。MATLAB所提供的多项式转换成嵌套形式函数指令格式为：

g= horner(f)                %将多项式f转换成嵌套形式g

输入以下的命令行进行举例说明：

>>syms x 
>> f1=2*x^6-5*x^5+3*x^4+x^3-7*x^2+7*x-20;
>> g1=horner(f1)               %将一维多项式f1转换成嵌套形式g1
g1 =
x*(x*(x*(x*(x*(2*x - 5) + 3) + 1) - 7) + 7) - 20

1.3.2. 符号多项式的向量表示形式

（1）以向量形式输入多项式

MATLAB提供了系数行向量的表达方式，其等同于输入了多项式f，相比于符号的表达形式则多项式向量的输入更为简洁。

输入以下的命令行进行举例说明：

>>syms x a b c
>> m=a*x^2+b*x+c;          %以符号方式输入一个一元多项式m
>> p=[a b c]
p =
 [ a, b, c]                  %输入系数向量用来代表一个一元多项式p ；
f=poly2sym(p)           %依照系数向量p写出x为变元的符号多项式
 f =
 a*x^2 + b*x + c

1.3.3. 反函数和复合函数求解

（1）单自变量函数求反函数的指令

格式如下：

     g=finverse(f)                  % 对原函数f 的默认变量求反函数g

输入以下的命令行进行举例说明：

>>syms x
>> f1=2*x^2+3*x++1
>> g1=finverse(f1)
Warning: finverse(2*x^2+3*x+1) is not unique.
> In sym.finverse at 43          %运行过程中警示其反函数值不止一个
g1 =
-3/4+1/4*(1+8*x)^(1/2)         %对反函数g的定义域需定义一个主值范围

（2）多自变量函数求反函数的指令

格式如下：

     g=finverse(f,v)                  % 对原函数f 的指定变量v求反函数g

输入以下的命令行进行举例说明：

>> syms t x a b
>> f1=b*exp(-t+a*x);
>> g1=finverse(f1,t)             % 对原函数f1 的指定变量t求反函数g1
g1 =a*x-log(t/b)

继续输入：

>> g2=finverse(f1)               % 对原函数f1 的默认变量x求反函数g2
g2 = (t+log(x/b))/a

格式如下：

g=finverse(f,v)                  % 对原函数f 的指定变量v求反函数g

输入以下的命令行进行举例说明：

>> syms t x a b
>> f1=b*exp(-t+a*x);
>> g1=finverse(f1,t)             % 对原函数f1 的指定变量t求反函数g1
g1 =a*x-log(t/b)

继续输入：

>> g2=finverse(f1)               % 对原函数f1 的默认变量x求反函数g2
g2 = (t+log(x/b))/a

（3）f(g(y))形式的复合函数

k1=compose(f,g)            %复合法则是g(y)代入f(x)中x所在的位置
k2=compose(f,g,t)       %g(y)代入f(x)中x所在的位置，变量t再代替y

输入以下的命令行进行举例说明：

>> syms x y t
>> f=x*exp(-t) ;
>> g=sin(y) ;
>> k1=compose(f,g)
k1 =sin(y)*exp(-t)
继续输入：
>> k2=compose(f,g,t)
k2 =sin(t)*exp(-t)

2. 符号微积分运算

2.1. 函数的极限

(1) 求函数极限的指令格式

limit(f,x,a)                    %相当于数学符号
limit(f,a)                      %求函数f极限，只是变元为系统默认
limit(f)                       %求函数f极限，变元为系统默认，a取0
limit(f,x,a,’right’)               %求函数f右极限（x右趋于a）
limit(f,x,a,’left’)                %求函数f左极限（x左趋于a）

输入以下的命令行进行举例说明：

已知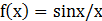，求

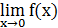
>> syms x
>> limit(sin(x)/x)               
ans =
1

（2）一维函数的泰勒级数展开

    taylor(f,x,a)             %将函数f在x=a处展开成5阶（默认）的泰勒级数
    taylor(f,x)                %将函数f在x=0处展开成5阶泰勒级数
    taylor(f)                  %将函数f在默认变量为0处展开成5阶泰勒级数

此外，以上指令格式中还可以添加参数，指定ExpansionPoint（扩展点），Order（阶数），OrderMode（阶的模式）等计算要求，其格式如下：

taylor(f,x,a, 'PARAM1',val1,'PARAM2',val2,...)

输入以下的命令行进行举例说明：

syms x y z
>> f=exp(-x)
>> h1=taylor(f)
h1 =- x^5/120 + x^4/24 - x^3/6 + x^2/2 - x + 1

继续输入：

>> h2=taylor(f,'order',7)
h2 =x^6/720 - x^5/120 + x^4/24 - x^3/6 + x^2/2 - x + 1

继续输入：

>> h3=taylor(f,'ExpansionPoint',1,'order',3)
h3 =exp(-1) - exp(-1)*(x - 1) + (exp(-1)*(x - 1)^2)/2

MATLAB还可以求二维函数的泰勒级数展开。

2.2. 求函数导数的命令

（1）单变量函数求导

diff(f,x,n)                    %计算f对变量x的n阶导数
diff(f,x)                     %计算f对变量x的一阶导数
diff(f,n)                     %计算f对默认变量的n阶导数
diff(f)                       %计算f对默认变量的一阶导数

输入以下的命令行进行举例说明：

>> syms x a
>> f=a*x^5
>> g1=diff(f)
g1 =5*a*x^4

继续输入：

>> g2=diff(f,2)
g2 =20*a*x^3

（2）多元函数求偏导

diff(f,x,y)                     %计算f对变量x偏导数，再求对变量y偏导
diff(f,x,y,z)                    %求x偏导数，再求y偏导，然后再求z偏导

输入以下的命令行进行举例说明：

>>syms x y z a b c
>> f=sin(a*x^2+b*y^2+c*z^2)
>> h1=diff(f,x)
h1 =2*a*x*cos(a*x^2 + b*y^2 + c*z^2)
>> h2=diff(f,x,y)
h2 =-4*a*b*x*y*sin(a*x^2 + b*y^2 + c*z^2)
>> h3=diff(f,x,y,z)
h3 =-8*a*b*c*x*y*z*cos(a*x^2 + b*y^2 + c*z^2)

2.3. 符号积分运算

（1）求函数积分的命令

int(S,v,a,b)             %求函数S对指定变量v在[a，b]区间上的定积分
int(S,a,b)                %求函数S对默认变量在[a，b]区间上的定积分
int(S,v)                   %求函数S对指定变量v的不定积分
int(S)                      %求函数S对默认变量的不定积分

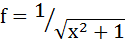【例】求函数的原函数。

输入以下的命令行进行解题：

>>syms x
>> f=(x^2+1)^(-1/2)
>> g=int(f)                    %求f的不定积分便可以求出f的原函数
g =
asinh(x)

因而函数f的原函数是函数g：g = asinh(x)+C

【例】求定积分的值。

输入以下的命令行进行解题：

>>syms x
>> f=(1/sqrt(2*pi))*exp(-x^2/2)
>> int(f,0,inf)
ans =
   (7186705221432913*2^(1/2)*pi^(1/2))/36028797018963968

得到的是一个计算式而非一个数，需要再做一次计算从而得到一个确切的数继续输入：

>> (7186705221432913*2^(1/2)*pi^(1/2))/36028797018963968
ans =
    0.5000

（2）双重积分和三重积分运算举例

【例】求由方程确定的园面积。

输入以下的命令行进行解题：

>> syms x y
>> S=int(int(1,y,-sqrt(1-x^2),sqrt(1-x^2)),x,-1,1)
S =
pi

所求面积公式为：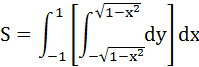

需要说明的是算法是由人设计的，即本题中的计算公式先由人推导出，其后交由MATLAB进行计算。当然，本题中求面积的算法不是唯一的，下例的三重积分其算法就可以更多了。

3. 符号方程求解

3.1. 符号代数方程求解

（1）单变量符号方程求解

可采用的函数指令格式如下：

S = solve(eqn1)

%求解方程eqn1关于默认变量的符号解S，所谓默认变量可由symvar(eqn1)找寻；

S = solve(eqn1,var1)

%求解方程eqn1关于指定变量var1的符号解S；

输入以下的命令行进行举例说明：

>> syms a b x y 
>> eqn1=a*sin(x)==b
eqn1 =
a*sin(x) == b

继续输入：

>> S=solve(eqn1)             %求解方程eqn1关于指定变量x的符号解S
S =  asin(b/a)                    %注意只给出了两个解 
pi - asin(b/a)

很明显，答案中只给出了两个解，这是需要进一步的分析的。此时可以在函数指令中加入参数：'ReturnConditions'，参数默认值为false，若取为true时则额外提供两个参数。

使用格式及应用举例说明如下：

>> [S,params, conditions]=solve(eqn1,'ReturnConditions',true)
S = asin(b/a) + 2*pi*k
   pi - asin(b/a) + 2*pi*k
params =k
conditions =a ~= 0 & in(k, 'integer')
         a ~= 0 & in(k, 'integer')

（2）多变量符号方程组求解

可采用的函数指令格式如下：

[Svar1,Svar2,...,SvarN] = solve(eqn1,eqn2,...,eqnM,var1,var2,...,varN)

为了避免求解方程时对符号解产生混乱，需要指明方程组中需要求解的变量var1，var2，...，varN，其所列的次序就是slove返回解的顺序，M不一定等于N。输入以下的命令行进行举例说明：

>> syms a b x y
>> eqn2=x-y==a
>> eqn3=2*x+y==b
[Sx,Sy]=solve(eqn2,eqn3,x,y)
Sx =a/3 + b/3
Sy =b/3 - (2*a)/3

3.2. 符号常微分方程求解

(1) 单个符号常微分方程求解

MATLAB提供的dsolve函数指令使用格式如下：

S=dsolve(eqn,'cond','v')

%上列函数指令对微分方程eqn在条件cond下对指定的自变量v进行求解。其中自变量v省略不写，自变量默认为t，或在符号声明中指出自变量；cond是初始条件，也可省略，而所得解中将出现任意常数符C，构成微分方程的通解；eqn为微分方程的符号表达式，方程中D被定义为微分，则D2、D3被定义为二阶、三阶微分，y的一阶导数dy/dx或dy/dt则可定义为Dy。

【例】求解下列常微分方程，已知初始条件：

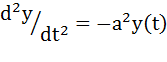
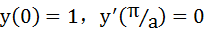
>> syms y(t) a                  %定义函数y及自变量t
>> Dy=diff(y)                  %定义Dy为t的一阶导数
Dy(t) =diff(y(t), t)
>> D2y=diff(y,2)              %定义D2y为t的二阶导数
D2y(t) =diff(y(t), t, t)

继续输入：

>> yt=dsolve(D2y==-a^2*y, y(0) == 1, Dy(pi/a) == 0)
yt =exp(-a*t*1i)/2 + exp(a*t*1i)/2

%请注意微分方程及初始条件的格式，均为符号表达式而非字符串形式。符号表达式中的等号应采用关系运算符“==”。

（2）符号常微分方程组的求解

符号常微分方程组的求解仍然使用dsolve函数指令，其使用格式如下：

[Sv1,Sv2,…]=dsolve(eqn1, eqn2,…,'cond1', 'cond2',…,'v1', 'v2',…)

%上列使用格式中，[Sv1,Sv2,…]为返回的解，eqn1, eqn2,…为常微分方程组，最大可包含12个常微分方程，均以符号表达式形式填入。'v1', 'v2',…为指定的自变量，也可以在符号声明中指出自变量及其函数。'cond1', 'cond2',…是初始条件，即可以是符号表达式形式也可以是字符串形式填入。

【例】求解下列常微分方程组，已知初始条件：

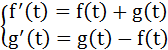
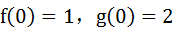
解如下：

>> syms f(t) g(t)
>> Df=diff(f)
Df(t) =diff(f(t), t)
 继续输入：
>> Dg=diff(g)
Dg(t) =diff(g(t), t)

继续输入：

>>  [sf,sg]=dsolve(Df==f+g,Dg==g-f,f(0)==1,g(0)==2)
sf =exp(t)*cos(t) + 2*exp(t)*sin(t)
sg =2*exp(t)*cos(t) - exp(t)*sin(t)   %注意两个返回解的先后次序

3.3. 符号运算应用举例

【例】求符号矩阵的行列式，逆和特征根。

解：在MATLAB命令窗口中直接输入下列命令行求行列式：

>> syms a b c d 
>> A=[a b;c d];
>> D=det(A)
D =a*d - b*c
>> B=inv(A)
B = [  d/(a*d - b*c), -b/(a*d - b*c)]
[ -c/(a*d - b*c),  a/(a*d - b*c)]
>> S=eig(A)
S =
   a/2 + d/2 - (a^2 - 2*a*d + d^2 + 4*b*c)^(1/2)/2
   a/2 + d/2 + (a^2 - 2*a*d + d^2 + 4*b*c)^(1/2)/2

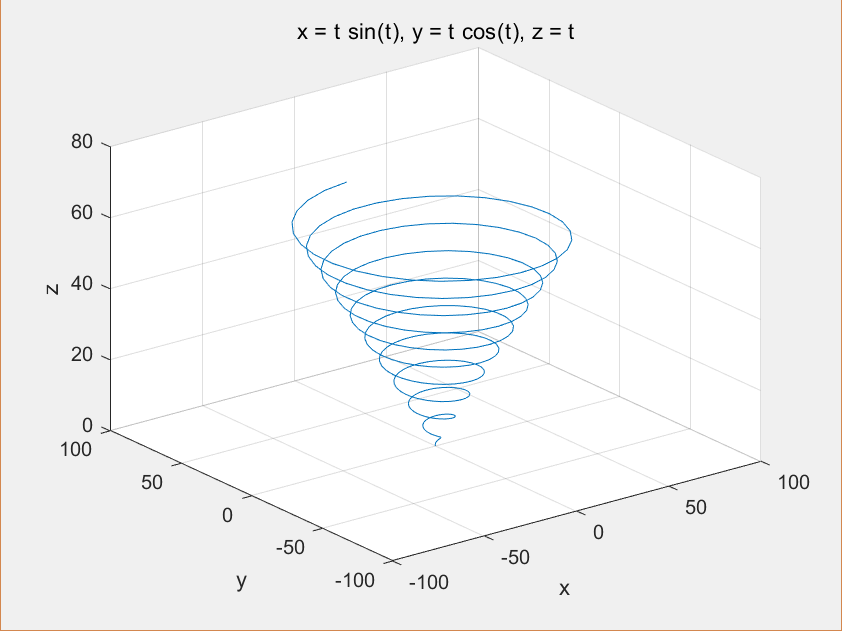
【例】绘制以下参数方程表示的三维图形，t的范围为

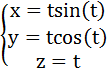
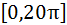
解：在MATLAB命令窗口中直接输入下列命令行绘制3D图；

>> syms t
>> ezplot3(t*sin(t),t*cos(t),t,[0,20*pi])

所绘制的图形如下：

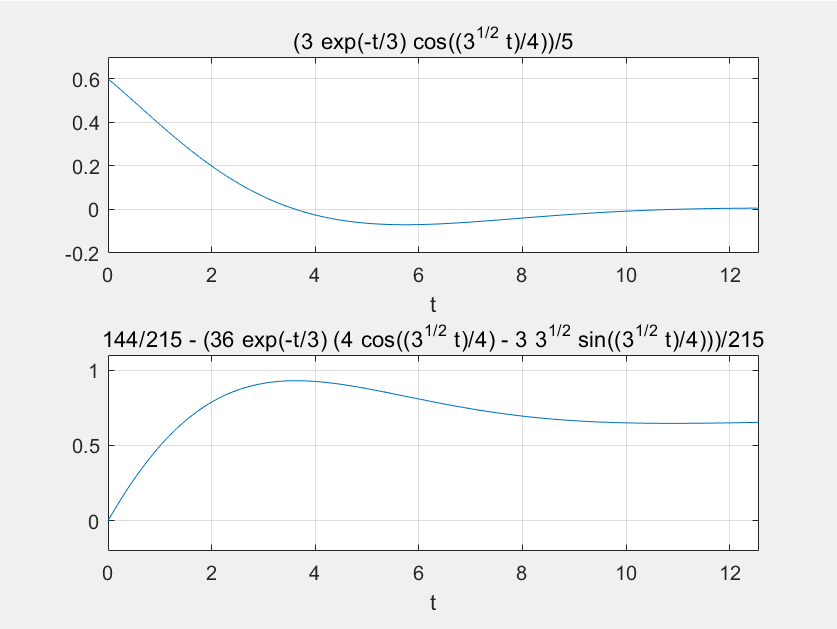
【例】绘制函数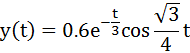及其积分上限函数的图形：

解：

syms t tao 
y=0.6*exp(-t/3)*cos(sqrt(3)/4*t); 
s=subs(int(y,t,0,tao),tao,t); 
subplot(2,1,1)
ezplot(y,[0,4*pi]),ylim([-0.2,0.7])
grid on 
subplot(2,1,2) 
ezplot(s,[0,4*pi]),ylim([-0.2,1.1])
grid on

Matlab基础02

1. MATLAB语言符号运算

1.1. MATLAB符号运算的概述

1.2. MATLAB符号对象的创建和使用

1.2.1. Matlab符号矩阵的创建

1.3. MATLAB符号多项式函数运算

1.3.1. 多项式函数的符号表达形式及相互转换

1.3.2. 符号多项式的向量表示形式

1.3.3. 反函数和复合函数求解

2. 符号微积分运算

2.1. 函数的极限

2.2. 求函数导数的命令

2.3. 符号积分运算

3. 符号方程求解

3.1. 符号代数方程求解

3.2. 符号常微分方程求解

3.3. 符号运算应用举例

results matching ""

No results matching ""

results matching ""

No results matching ""