第3章 计算机硬件系统
3.1 计算机的基本组成及工作原理
教学目的
掌握计算机系统的组成成分及各组成成分的功能
了解计算机的工作过程。
教学重点
- 计算机硬件组成及各部分功能
教学引入
现在,我们已经了解计算机的发展,那么计算机的内部有哪些部件组成?
3.1.1 计算机的基本组成
概念
硬件系统:指由电子部件和机电装置组成的计算机实体。
软件系统:指为计算机工作服务的全部技术资料和各种程序。
功能
- 硬件的功能:接受计算机程序,并在程序的控制下完成数据输入、数据处理和输出结果等任务。
- 软件的功能:保证计算机硬件的功能得以充分发挥,并为用户提供一个宽松的工作环境。
关系
- 二者缺一不可,没有软件的计算机称为“裸机”裸机不能做任何工作。
- 硬件是组成计算机的物质基础,软件则是其灵魂
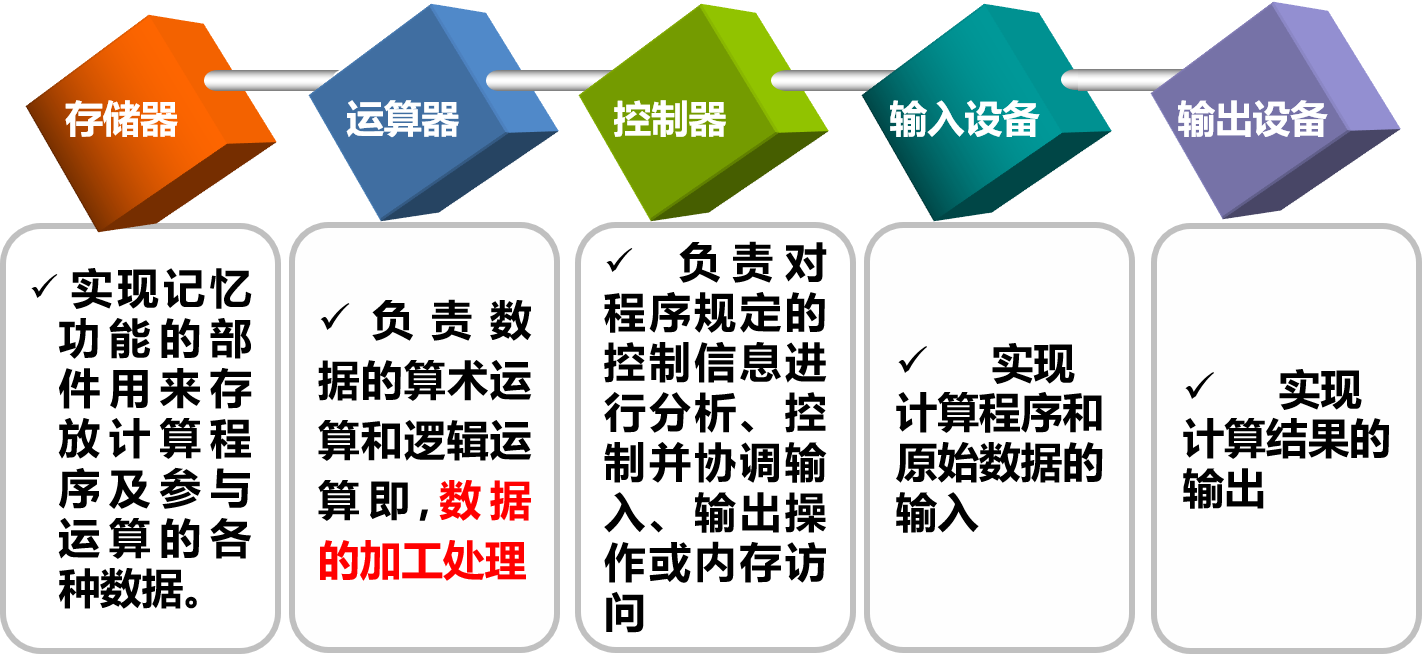
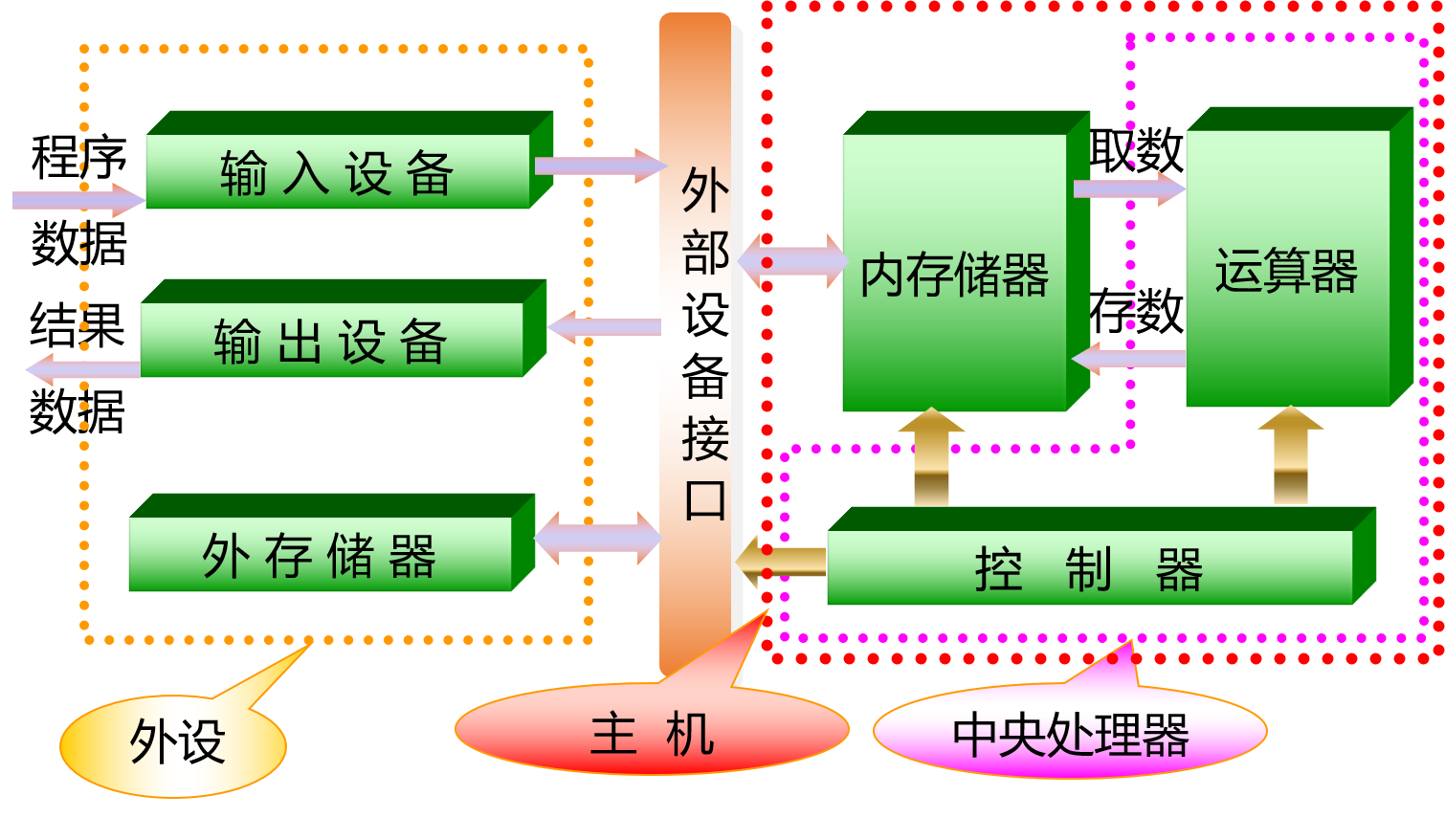
微型计算机的组成框图
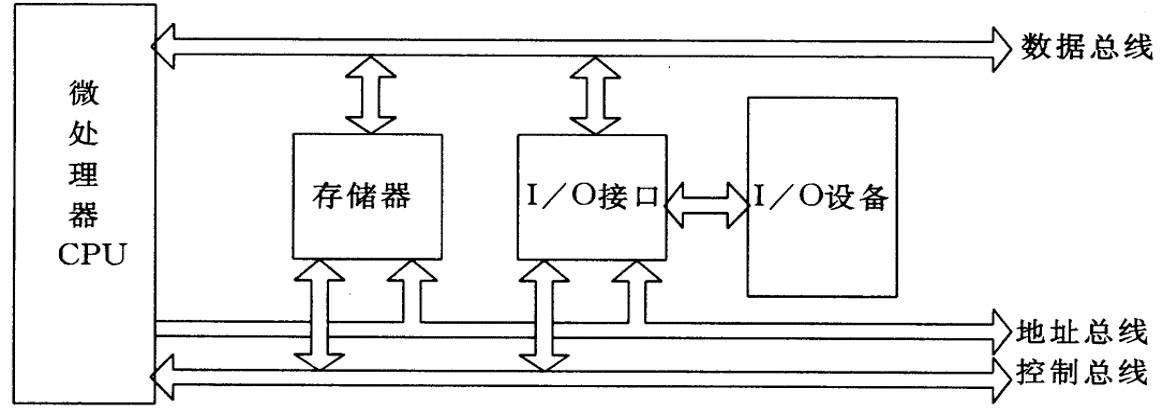
冯诺依曼型计算机两大特征:
程序存储
采用二进制
3.1.2 计算机的基本工作原理
指令
- 定义:能够被计算机识别的命令,是对计算机进行程序控制的最小单位
- 组成:
- 操作码:计算机应该执行的某种操作的性质和功能;
- 地址码:被操作的数据存放在何处,即指明操作数的地址
程序
- 由完成某一特定任务的一组指令所组成。
机器指令
- 要计算机执行某种操作的指令,它们全部由0和1这样的二进制编码组成,其操作通过硬件逻辑电路实现。
计算机的工作过程
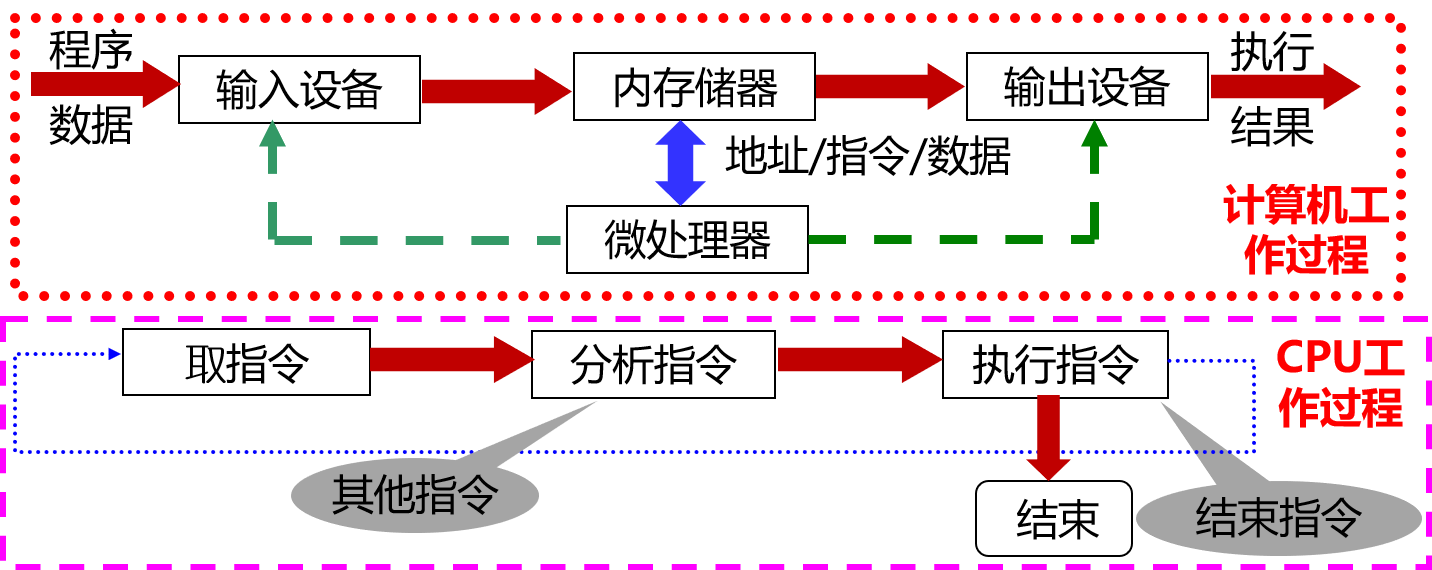
- 计算机的自动计算过程就是执行一段预先编制好的计算程序的过程;
- 计算程序是指令的有序集合。
指令的逐条执行是由计算机的硬件实现的,可归结为取指令、分析指令、执行指令所规定的操作,并为取下一条指令准备好指令地址。
教学小结
计算机系统的组成
计算机硬件及各部分的功能
计算机的工作过程
3.2 信息在计算机中的表示
教学目的
- 学习计算机中数据信息的表示方式和各种表示方式之间的内在联系、二进制的定点与浮点表示及其原码反码补码表示、计算机中非数值数据的编码,使大家对数值数据的表示方式有所了解。
教学重点
不同进制数之间的转换
二进制数的原码、反码及补码表示
- 字符编码
教学引入
- 计算机可以处理各种各样的数据,如文本、图像、声音、动画等,那么这些信息在计算机内部是如何保存的?
3.2.1 数值数据
- 表示数据信息的两种基本方法

十进制数
- 10个有序的数字符号:0,1,2,3,4,5,6,7,8,9
- 小数点符号:“.”
- “逢十进一”的计数规则
- 其中:“十” 为进位基数(Base / Radix)
简称基数( R )。
表示法
并列表示法 Positional Notation

如上所示,处在不同位置的数字具有不同的“权”,并列计数法,也称位置表示法。
多项式表示法 Polynomial Notation
将并列式按“权” 展开为按权展开式,称为多项 式表示法。如下例:
1、进位制数及其相互转换
进位制数
- 所谓“数制”,即各种进位计数制。
在R进制中,具有
- $个数字符号,它们是
- 在R进制中,由低位向高位是按“逢R进一“的规则进行计数。
- R进制的基数(base)是 R,R进制数的第i位的权(weight)为,并约定整数最低位的位序号。
小数点右移一位扩大倍,左移一位缩小为原来的倍。
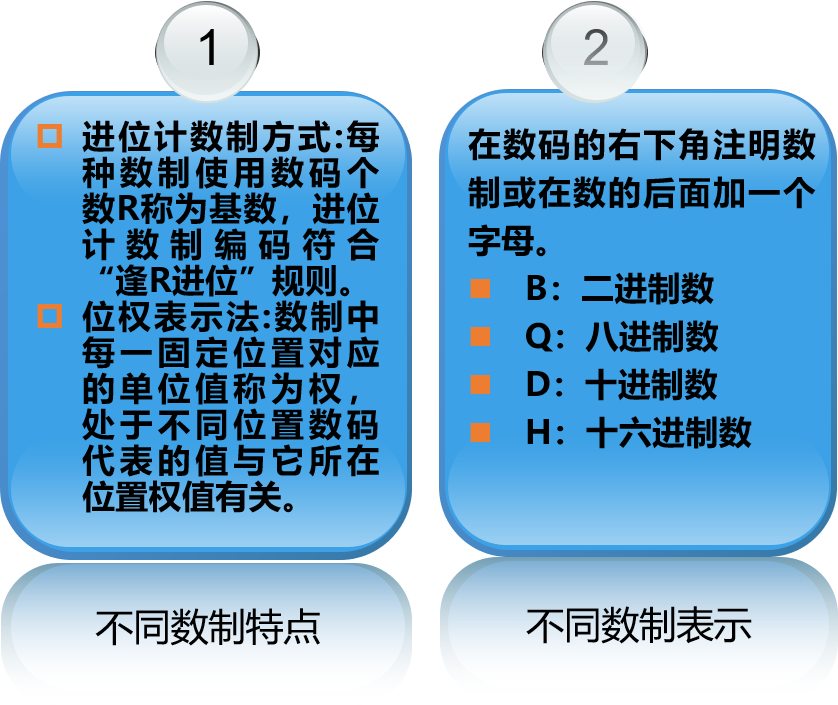
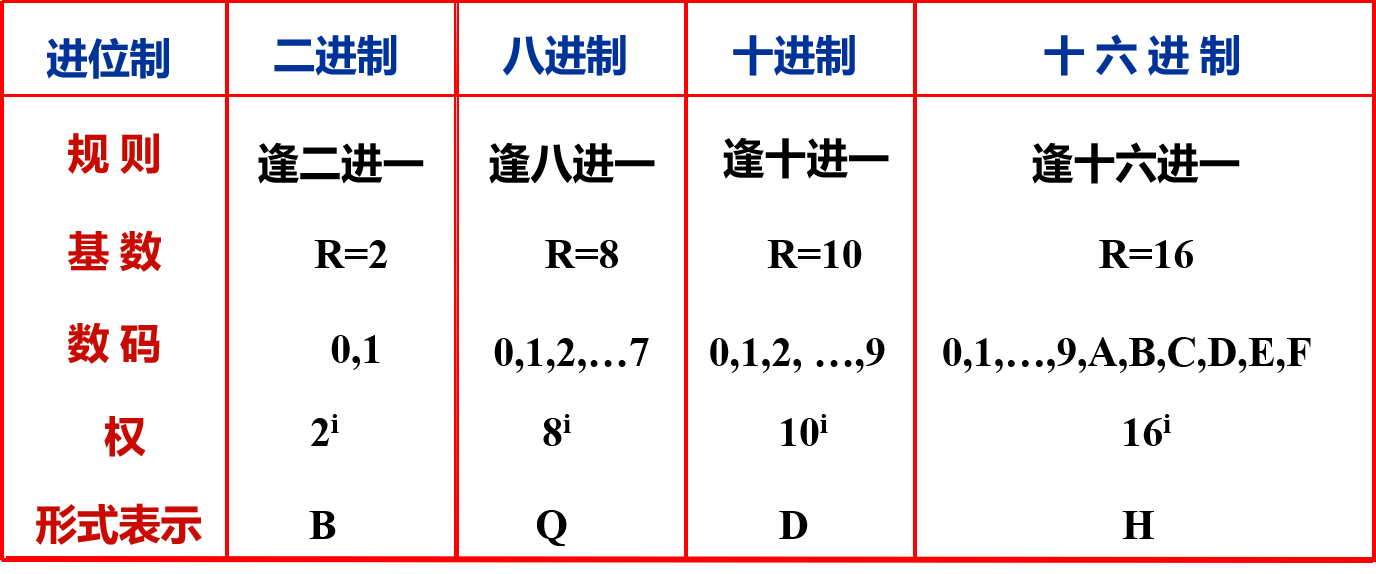
计算机中常用进制数的表示

例1:求的等值十进制数。
分析:使用按权相加法,即将各位进制数码与它对应的权相乘,其积相加,和数即为与该R进制数相对应的十进制数。 即
例2:求等值二进制数
解:先求等值二进制数
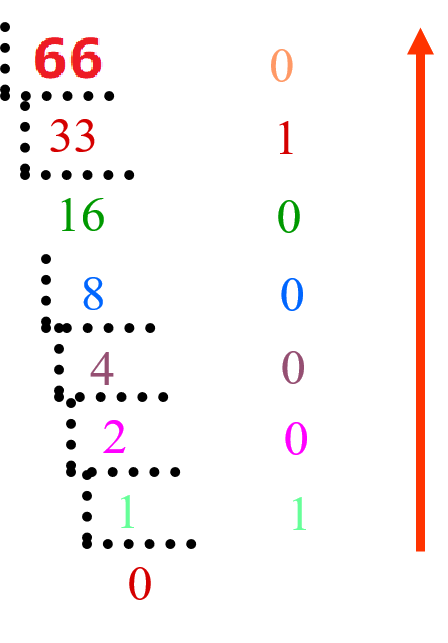
即
再求小数部分 积的整数部分
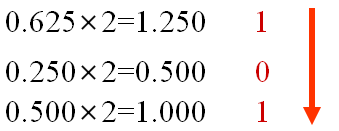
即
所以:
注意:十进制小数不一定都能转换成完全等值的二进制小数,所以有时要取近似值,有换算误差存在
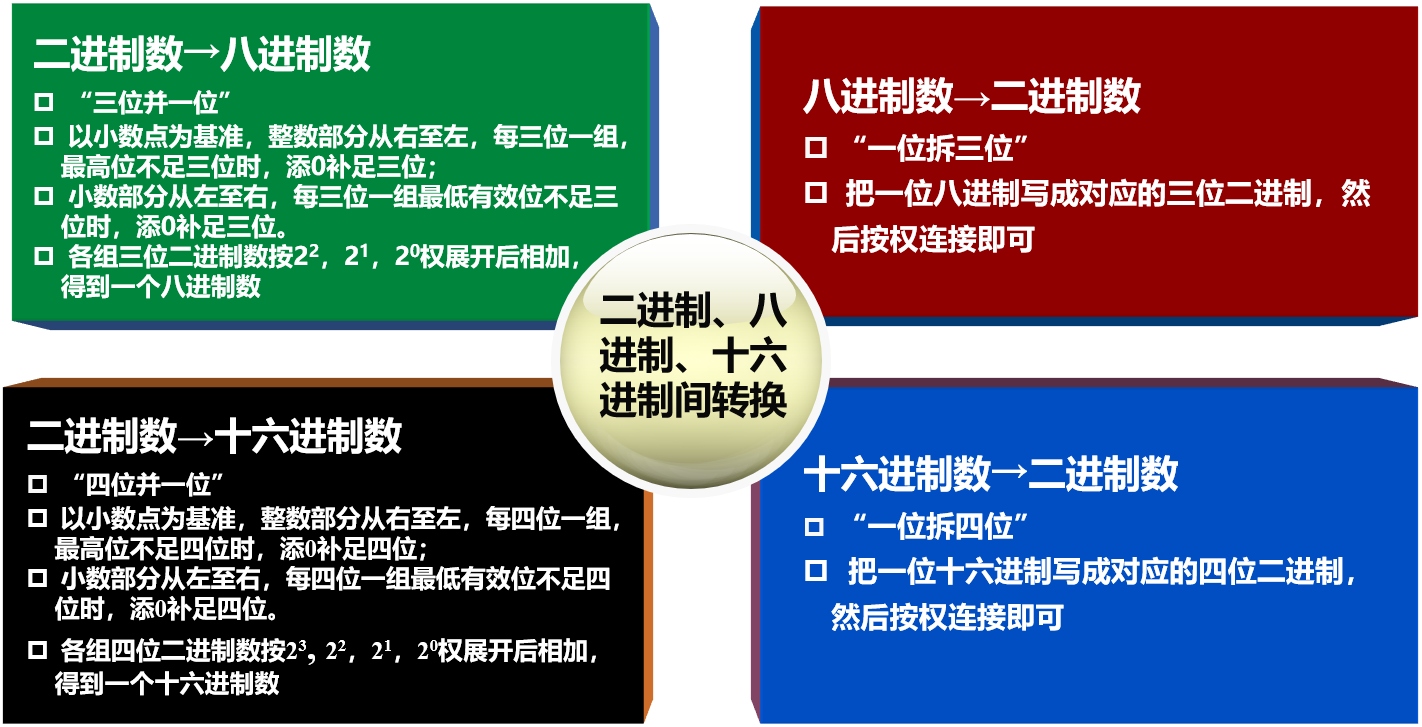
例3:将 为八进制数。
分析:按照“三位并一位”的原则,对二进制数进行处理。
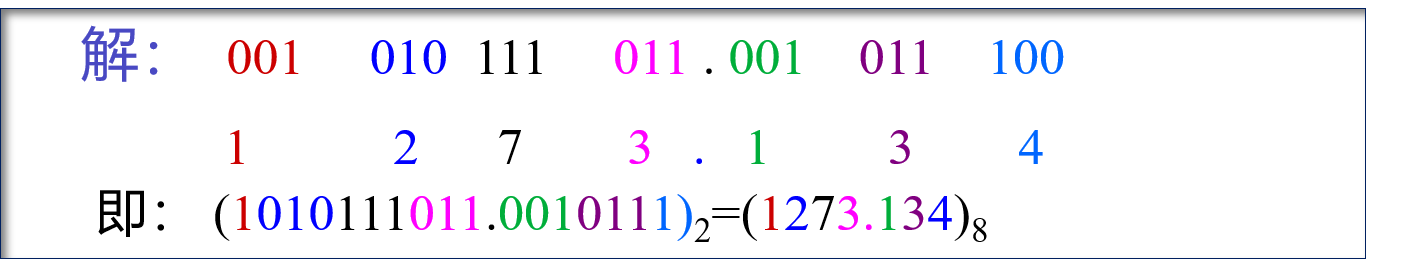
例4:将转换成二进制数

例5:将转换成十六进制数
分析:按照“四位并一位”的原则,对二进制数进行处理。

例6:将$转换成二进制数
分析:按照“一位拆四位”的原则,对八进制数进行处理。

课堂练习
下列十进制数分别转换为二、八、十六进制
下列二进制数分别转换为八、十、十六进制
下列八进制数分别转换为二、十、十六进制
- 下列十六进制数分别转换为二、八、十进制
答案:
下列十进制数分别转换为二、八、十六进制
下列二进制数分别装换为八、十、十六进制
下列八进制数分别转换为二、十、十六进制
下列十六进制数分别转换为二、八、十进制
2、二进制数的定点表示
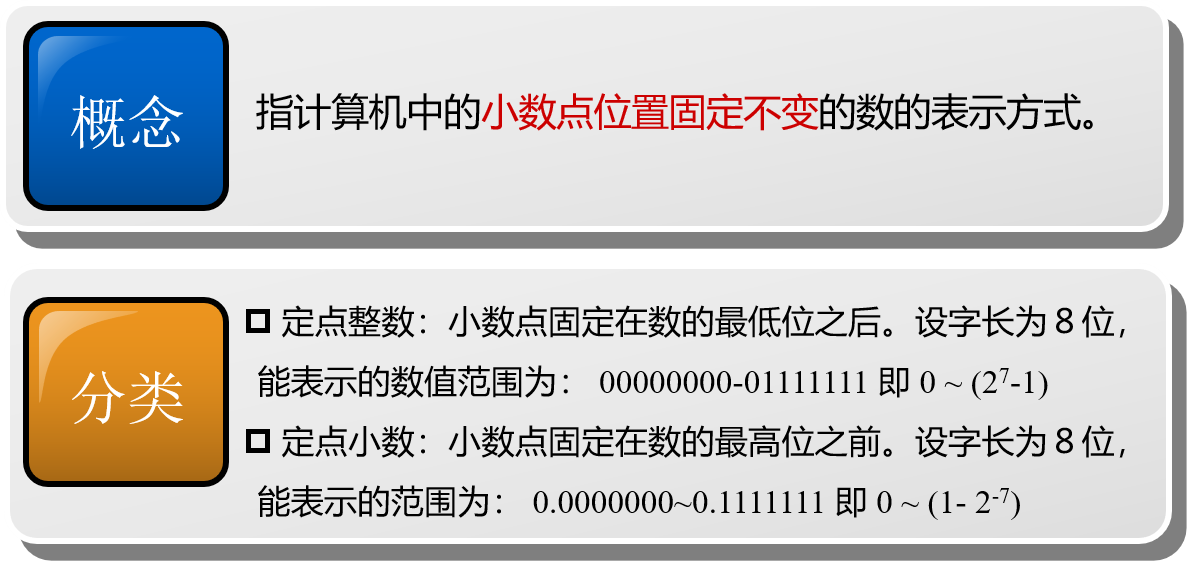
浮点表示法: 指计算机中的小数点位置不是固定的,或者说是“浮动” 的
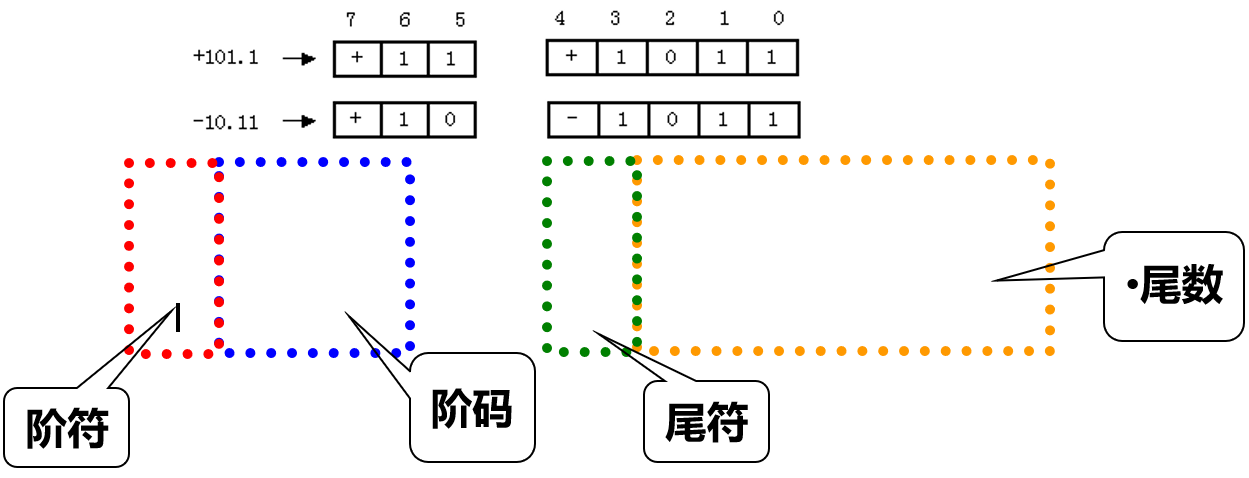
数的表示方式:通过阶码和尾数表示:
E称为阶码,它是一个二进制正整数 ;
- E前的±为阶码的符号,称为阶符({% math %} E_f {% endmath %});
- S称为尾数,它是一个二进制正小数 ;
S前的±为尾数的符号,称为尾符({% math %} S_f {% endmath %}) ;
“2”是阶码E的底数。
例:二进制数+101.1和-10.11的浮点表示形式为

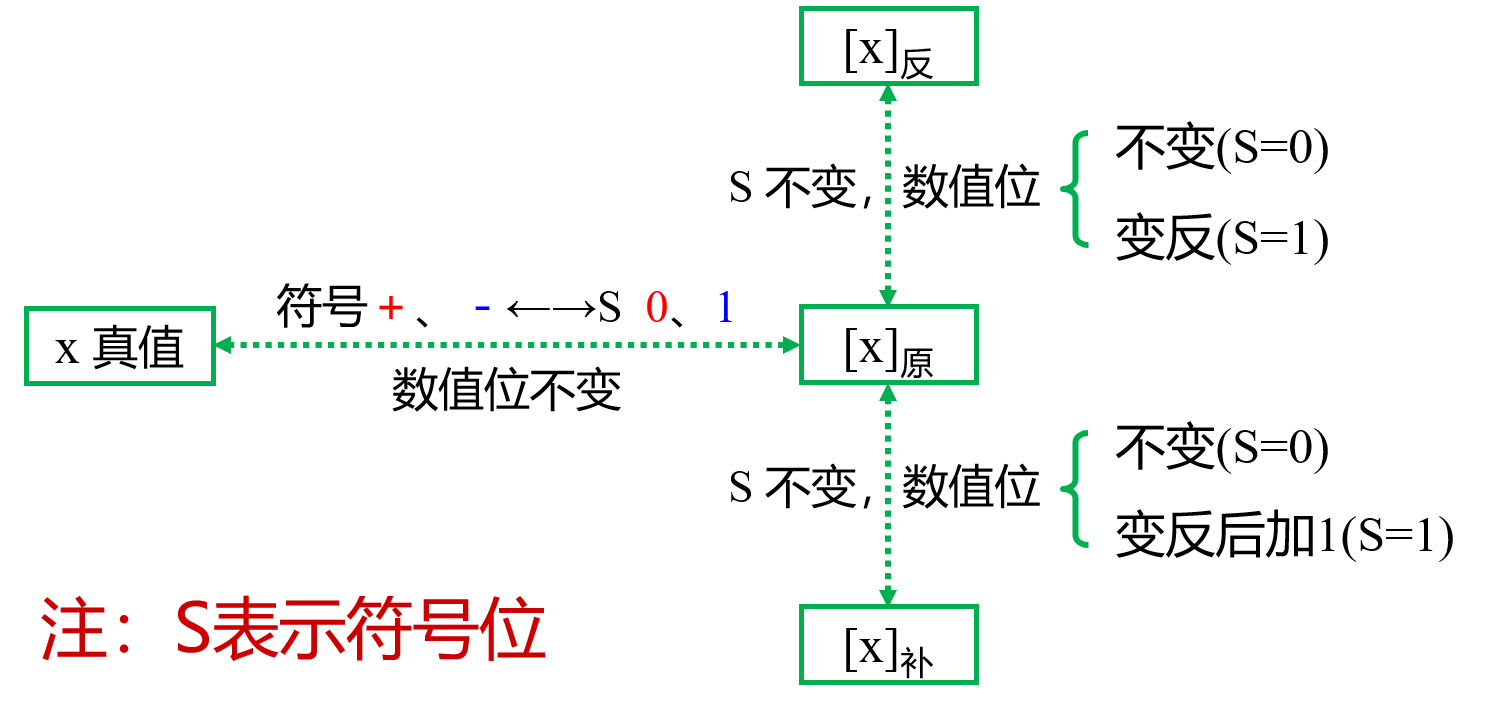
3. 二进制的原码、反码及补码表示
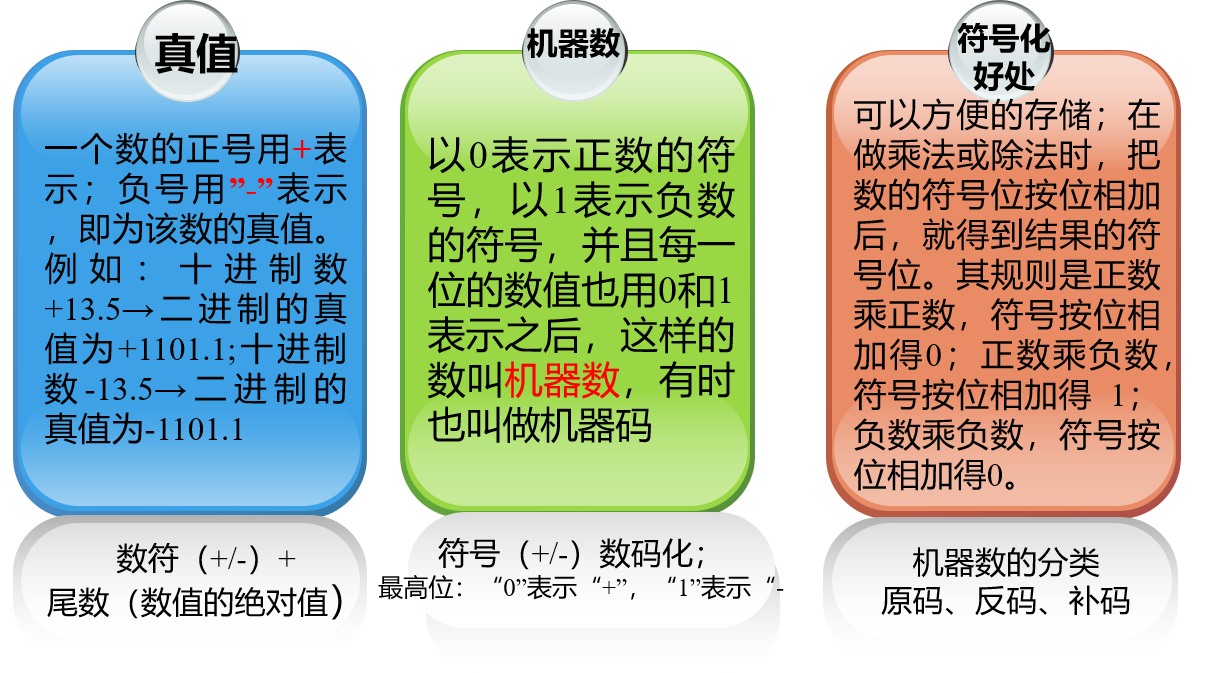
原码表示法
符号位+尾数部分(真值)
原码是一种机器数。数的原码表示是在机器中用符号位的0和1表示数的正号和负号,而其余位表示数的本身。
对于正数,,则原码为:
对于负数,,则原码为:
原码表示法的特点:
- 优点:简单易懂,与真值的转换方便。
- 缺点:异号相加时机器首先应判断数的符号,然后比较两数的绝对值,增加了机器的复杂程度。
反码表示法
正数:尾数部分与真值形式相同;
负数:尾数为真值数值部分按位取反
表示方法
对于正数其反码与原码相同;对于 则反码为:
对于负的二进制数,符号位不变,数值各位取反,即 0变为1,l变为0。
对于,则反码为
特点:
- 在计算机中容易实现,如触发器,一边表示原码,另一边表示反码
什么是补码?
(+4)称为(−8)对12的补码,
数学公式表示为:
补码表示法
正数:尾数部分与真值形式相同;
负数:尾数为真值数值部分按位取反加1
表示方法
对于正数其补码与原码相同;对于 则补码为:
对于负数,除了符号位之外数值各位取反,末尾位加1。对于 则补码为:
特点:
- 负数用补码表示时,可把减法转化成加法,可以用加法器实现减法,简便、经济
例7:已知计算机字长为8位,试写出二进制+101010和-101010的机器中表示的原码、反码和补码。
解:设该机器采用定点整数表示,则其真值形式为:
例8:已知,求真值X
解:先由求出,则得:
的符号位为1,故其所对应的真值为负,且数值为
的各位取反,即:
4、信息的存储单位
什么是编码?
所谓编码(code),是指按一定规则组合而成二进制数码序列来表示数字符或其他符号。
计算机中常用的编码有十进制编码(BCD码)、可靠性编码(校验码)字符编码、操作编码及汉字编码等。
BCD码(二→十进制码)
- 用四位二进制代码对一位十进制数进行编码,它既具有二进制码的形式(四位二进制码),又有十进制数的特点(每四位二进制码是一位十进制数)
例:
解:
↓ ↓ ↓
- 课堂交互
问题:已知,求其对应的BCD编码?
3.2.2 字符数据
汉字的机内码
- 交换码:用于汉字外码和内部码的交换。
- 国标码:是国家规定的用于汉字信息处理使用的代码的依据。国标码是双字节代码,国标码中的每个字符用两个字节进行编码,每个字节的低7位表示信息,最高位为0。
- 汉字的机内码:是供计算机系统内部进行存储、加工处理传输统一使用的代码。目前使用最广泛的是变形的国标码 将
`GB2312-80交换码的两个字节的最高位分别置为1而得到的。
汉字编码
- 汉字字形码:是指汉字字形点阵的代码, 用于汉字的显示和打印。目前汉字字形的产生方式大多是数字式,即以点阵方式形成汉字。
- 汉字字库:是汉字字形数字化后, 以二进制文件形式存储在存储器中而形成的汉字字模库。
- 软汉字字库:汉字字库文件存储在软盘或硬盘中。
硬汉字字库:亦称汉卡,汉字字库存储在汉卡中,将汉卡安装在机器的扩展槽中。

3.2.3 声音数据
声音是一种连续的随时间变化的波,即声波。用连续波形表示声音的信息,称为模拟信息。
声音在计算机内表示时需要把声波数字化,又称量化。
- 在每一固定的时间间隔里对声波进行采样,采得的波形称为样本,再把样本(振幅的高度)量化成二进制代码存储在机内。这个过程称为声音的离散化或数字化,也称模/数转换。
- 反之,将声音输出时,要进行逆向转换,即数/模转换。
- 常用的声音文件扩展名为.wav,.au,.voc和.mp3
3.2.4 图像和图形信息的表示
颜色表示法:在计算机中,用RGB值来表示颜色。
数字化图像和图形
- 位图图像:计算机通过指定每个独立的点(或像素)在屏幕上的位置来存储位图图像。位图图像文件的扩展名为.bmp,.pcx,.tif,.jpg和.gif。
- 矢量图形:由一串可重构图形指令构成。矢量图形文件的扩展名为.wmf,.dxf,.mgx和.cgm。
3.3 运算基础
教学目的
本讲主要介绍二进制与十进制的算术运算以及二进制的逻辑运算的基本知识,通过本讲的学习使大家对计算机中的基本运算方法有所了解。
教学重点
二进制补码运算
二进制的逻辑运算
教学引入
1+1=2
1+1=10
1+1=1

3.4 逻辑代数与逻辑电路
教学目的
- 本讲主要介绍分析和设计逻辑电路所用的数学工具——逻辑代数的基本知识,并简要介绍计算机中常用的几种逻辑电路。
教学重点与难点
- 逻辑代数中的常用公式;
- 逻辑代数的简单应用;
教学引入
- 计算机内部处理的是0、1信息,具体到计算机内部的硬件如何处理这些信息?
3.4.1 逻辑代数的初步知识
- 数字电路的特点及描述工具
- 数字电路是一种开关电路;
- 输入、输出量是高、低电平,可以用二元常量$(0,1)$来表示。
- 输入量和输出量之间的关系是一种逻辑上的因果关系。
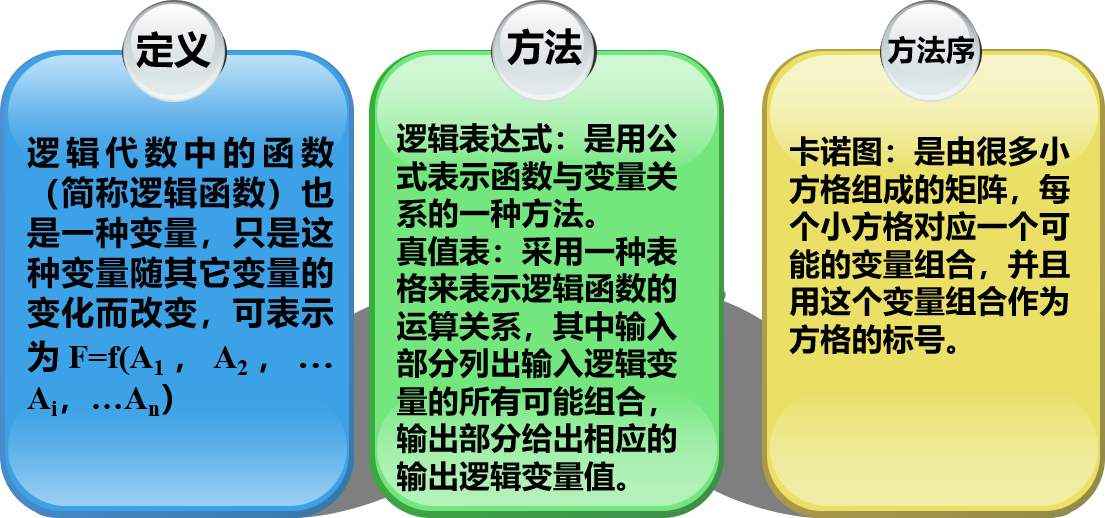
- 仿效普通函数的概念,数字电路可以用逻辑函数的的数学工具来描述。
- 逻辑变量
- 逻辑代数是一种双值代数,其变量只有0、1两种取值。
- 逻辑代数的变量简称逻辑变量,可用字母A、B、C等表示。
- 逻辑变量只有三种最基本的运算,即逻辑加、逻辑乘及逻辑非。
逻辑函数的简化
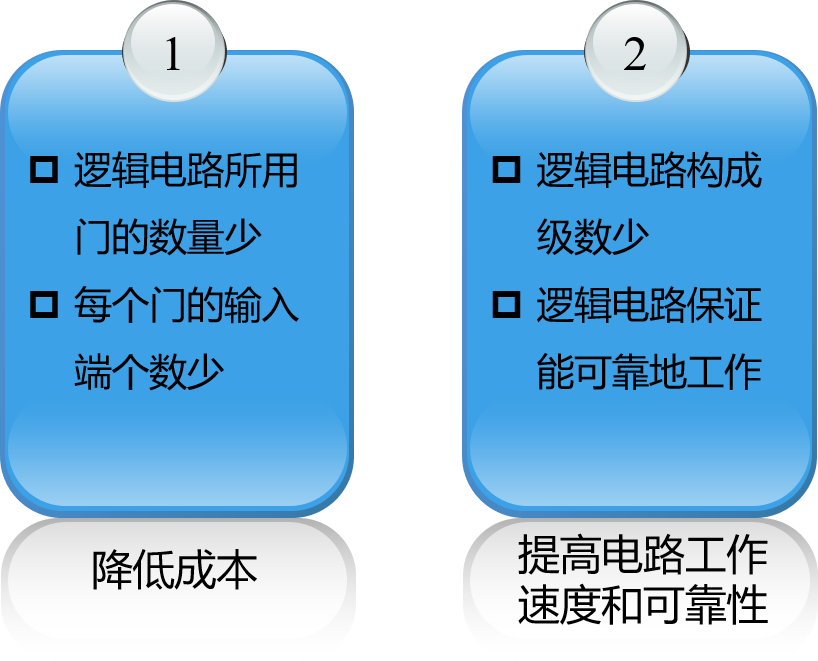
- 教学小结
- 逻辑代数中的常用公式;
- 逻辑代数的化简与证明
- 基本逻辑门电路的工作原理、逻辑符号及外特性;
- 组合门电路的实现原理与功能特性。