第2章 计算机基础知识
2.1 计算科学的典型问题
一、排序问题
将全班学生的考试成绩按分数由高到低排序:
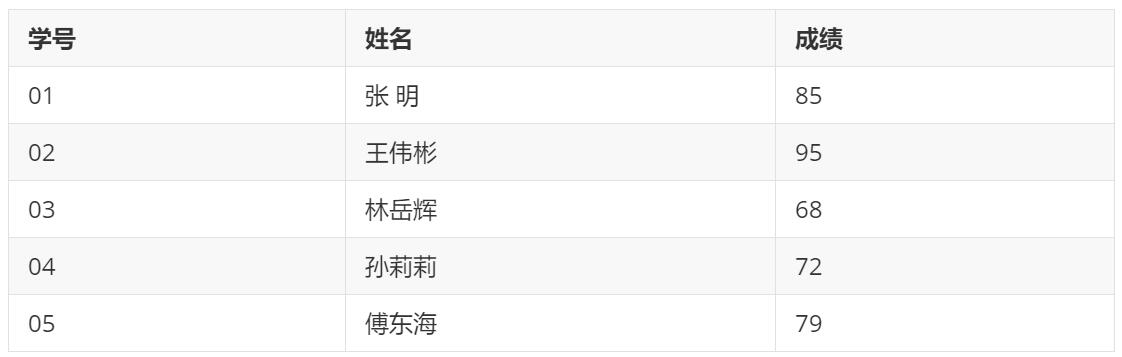
排序结果:
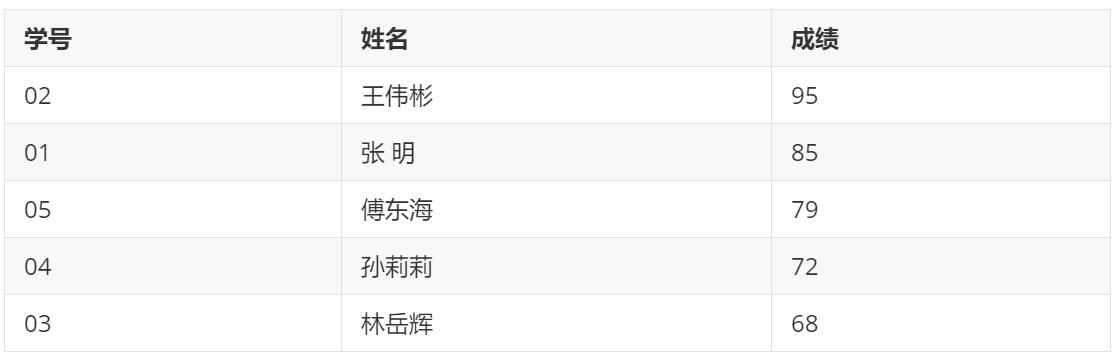
排序问题
按照一定的顺序创新排列数据项
常用的排序算法包括选择排序、冒泡排序、合并排序、快速排序等
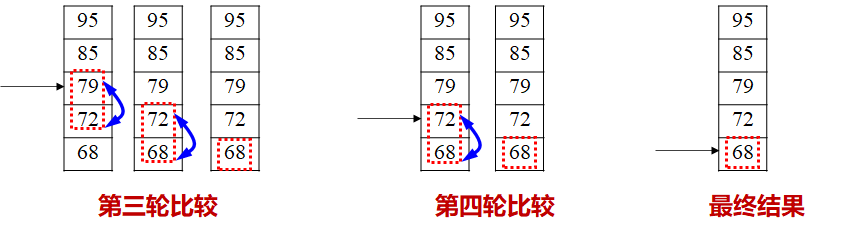
冒泡排序:将相邻的两个数比较,将小(大)的调到前头 (
以冒泡排序为例说明)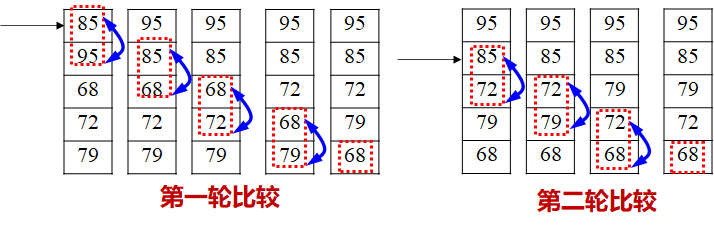
二、汉诺塔问题
设A,B,C是3个塔座。开始时,在塔座A上有一叠共n个圆盘,这些圆盘自下而上,由大到小地叠在一起。各圆盘从小到大编号为1,2,…,n。现要求将塔座A上的这叠圆盘移到塔座C上,并仍按同样顺序叠放。在移动圆盘时应遵守以下移动规则:
规则1每次只能移动1个圆盘;规则2任何时刻都不许将较大圆盘压在较小圆盘之上;规则3在满足移动规则1和2的前提下,可将圆盘移至A,B,C中任一塔座上
汉诺塔问题分析如果A柱上只有一个盘子,则A柱→C柱
如果A柱上有两个盘子,小盘A柱→B柱,大盘A柱→C柱,小盘B柱→ C柱
如果A柱上有n个盘子,将此问题简化为n-1个盘子和最下面的第n个盘子的情况
- n-1个盘子 A柱→B柱, 第n个盘子 A柱→C柱, n-1个盘子 B柱→C柱
- 问题转化移动n-1个盘子问题
C语言递归代码实现:#include <stdio.h> void move(char source, char target ){ printf(“%c → %c\t”, source, target); } void hanoi(int n, char source ,char temp, char target){ if(n==1) move(source , target); else{ hanoi(n-1,source,target,temp); move(source, target); hanoi(n-1,temp,source,target); } } void main(){ int n; printf(“输入盘子数:\n”); scanf(“%d”, &n); hanoi(n, ’A’, ’B’, ’C’); printf(“\n”); }
三、N皇后问题
国际象棋中的“皇后”在横向、纵向、和斜向都能走步和吃子,问在n×n 格的棋盘上如何能摆上n个皇后而使她们不能互相吃掉?
起源于古罗马帝国的权力制衡思想,当时的政治理论家波利比奥斯提出了该问题。
问题分析:
回溯法:- 方法起源于古希腊神话,英雄忒修斯消灭躲藏在迷宫中怪兽。

基本思想:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
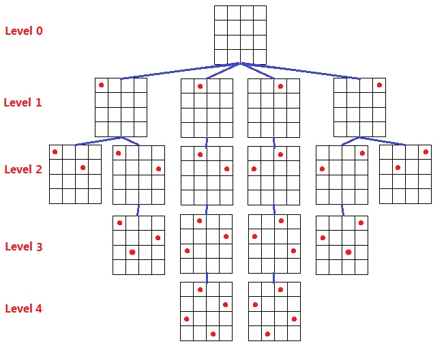
以四皇后为例:
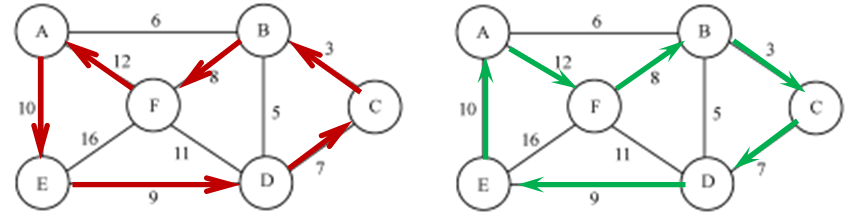
四、旅行商问题
- 设有n个城市,已知任意两城市间的距离,现有一推销员想从某一城市出发经过每一城市(且只经过一次)最后又回到出发点,问如何找一条最短路径?
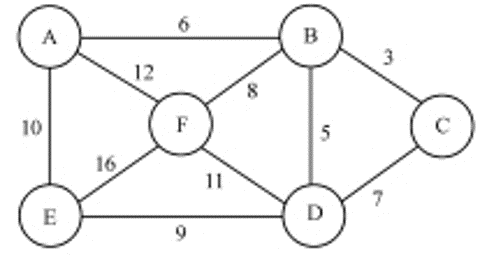
又称货郎担问题或旅行推销问题,即TSP问题(Traveling Salesman Problem),是运筹学领域中著名问题之一。
1859年,TSP问题由英国汉密尔顿爵士作为一个悬赏问题提出。
这个几分钟就可以理解的问题,延续至今未能够完成解决 {% math %} d(i,V')=\begin{cases} \min{i}[C{ik} + d(k,V'-{k})],& k\in V'\ C_{i0}, & i\neq 0 \and V' = \emptyset
\end{cases} {% endmath %}
动态规划

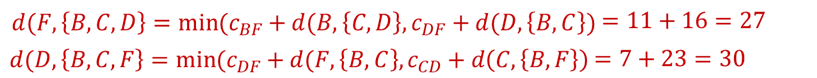
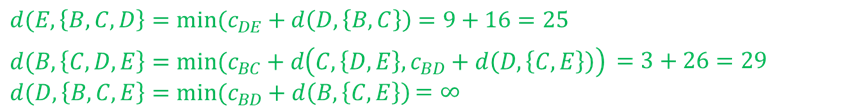
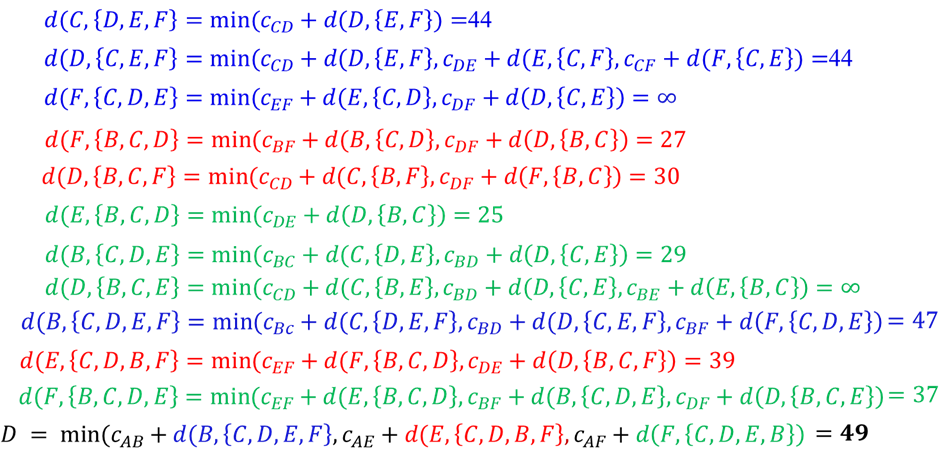
- TSP路径为: